
·ÖÎö £¨1£©ÏÈËã³Ë·½£¬ÔÙËã³Ë·¨£»
£¨2£©ÀûÓüӷ¨½»»»ÂÉÓë½áºÏÂÉ£¬½«·ÖĸÏàͬµÄ·ÖÊý½áºÏÔÚÒ»Æð£»
£¨3£©ÏÈËã³ý·¨£¬ÔÙËã¼Ó·¨£»
£¨4£©ÏȽ«¼õ·¨×ª»¯Îª¼Ó·¨£¬ÔÙ¼ÆËã¼Ó·¨¼´¿É£»
£¨5£©ÏÈËãÀ¨ºÅ£¬ÔÙ´Ó×óÍùÓÒÒÀ´Î¼ÆË㣻
£¨6£©ÏȽ«¼õ·¨×ª»¯Îª¼Ó·¨£¬ÔÙ¼ÆËã¼Ó·¨¼´¿É£»
£¨7£©ÀûÓó˷¨·ÖÅäÂɼÆË㣻
£¨8£©ÀûÓó˷¨·ÖÅäÂɼÆË㣻
£¨9£©ÏÈ°ÑËÄÏîÒ»×é½øÐмÆË㣬ÔÙÏà¼Ó¼´¿ÉÇó½â£®
½â´ð ½â£º£¨1£©-£¨-3£©2¡Á2
=-9¡Á2
=-18£»
£¨2£©$\frac{1}{2}$+£¨-$\frac{2}{3}$£©+$\frac{4}{5}$+£¨-$\frac{1}{2}$£©+£¨-$\frac{1}{3}$£©
=£¨$\frac{1}{2}$-$\frac{1}{2}$£©+£¨-$\frac{2}{3}$-$\frac{1}{3}$£©+$\frac{4}{5}$
=0-1+$\frac{4}{5}$
=-$\frac{1}{5}$£»
£¨3£©-82+72¡Â£¨-36£©
=-82-2
=-84£»
£¨4£©8+£¨-$\frac{1}{3}$£©-2.5-£¨+1$\frac{2}{3}$£©
=£¨8-2.5£©+£¨-$\frac{1}{3}$-1$\frac{2}{3}$£©
=5.5-2
=3.5£»
£¨5£©2$\frac{1}{2}$¡Á$\frac{1}{4}$¡Â£¨$\frac{1}{8}$-2£©
=$\frac{5}{2}$¡Á$\frac{1}{4}$¡Á£¨-$\frac{8}{15}$£©
=-$\frac{1}{3}$£»
£¨6£©£¨-5£©+£¨-6£©-£¨+12£©-£¨-7£©
=-5-6-12+7
=-23+7
=-16£»
£¨7£©11.8¡Á3$\frac{3}{4}$-£¨-11.8£©¡Á1.7-11.8¡Á$\frac{3}{4}$-11.8¡Á£¨-0.3£©
=11.8¡Á£¨3$\frac{3}{4}$+1.7-$\frac{3}{4}$+0.3£©
=11.8¡Á5
=59£»
£¨8£©£¨-5£©¡Á£¨-3$\frac{6}{7}$£©+£¨-7£©¡Á£¨-3$\frac{6}{7}$£©+12¡Á£¨-3$\frac{6}{7}$£©
=£¨-5-7+12£©¡Á£¨-3$\frac{6}{7}$£©
=0¡Á£¨-3$\frac{6}{7}$£©
=0£»
£¨9£©1-2-3+4+5-6-7+8+9-10-11+12+¡+2005-2006-2007+2008
=£¨1-2-3+4£©+£¨5-6-7+8£©+£¨9-10-11+12£©+¡+£¨2005-2006-2007+2008£©
=0£®
µãÆÀ ±¾Ì⿼²éµÄÊÇÓÐÀíÊýµÄÔËËãÄÜÁ¦£®×¢Ò⣺
£¨1£©ÒªÕýÈ·ÕÆÎÕÔËËã˳Ðò£¬ÔÚ»ìºÏÔËËãÖÐÒªÌرð×¢ÒâÔËËã˳Ðò£ºÏÈÈý¼¶£¬ºó¶þ¼¶£¬ÔÙÒ»¼¶£»ÓÐÀ¨ºÅµÄÏÈËãÀ¨ºÅÀïÃæµÄ£»Í¬¼¶ÔËËã°´´Ó×óµ½ÓÒµÄ˳Ðò£»
£¨2£©È¥À¨ºÅ·¨Ôò£º--µÃ+£¬-+µÃ-£¬++µÃ+£¬+-µÃ-£®



| Ä꼶 | ¸ßÖÐ¿Î³Ì | Ä꼶 | ³õÖÐ¿Î³Ì |
| ¸ßÒ» | ¸ßÒ»Ãâ·Ñ¿Î³ÌÍƼö£¡ | ³õÒ» | ³õÒ»Ãâ·Ñ¿Î³ÌÍƼö£¡ |
| ¸ß¶þ | ¸ß¶þÃâ·Ñ¿Î³ÌÍƼö£¡ | ³õ¶þ | ³õ¶þÃâ·Ñ¿Î³ÌÍƼö£¡ |
| ¸ßÈý | ¸ßÈýÃâ·Ñ¿Î³ÌÍƼö£¡ | ³õÈý | ³õÈýÃâ·Ñ¿Î³ÌÍƼö£¡ |
¿ÆÄ¿£º³õÖÐÊýѧ À´Ô´£º ÌâÐÍ£ºÌî¿ÕÌâ
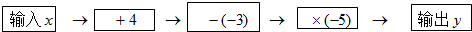
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º³õÖÐÊýѧ À´Ô´£º ÌâÐÍ£º½â´ðÌâ
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º³õÖÐÊýѧ À´Ô´£º ÌâÐÍ£º½â´ðÌâ
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º³õÖÐÊýѧ À´Ô´£º ÌâÐÍ£ºÑ¡ÔñÌâ
| A£® | x3-2x+2x2+5 | B£® | 5-2x+2x2-x3 | C£® | -x3+2x2+2x+5 | D£® | -x3+2x2-2x+5 |
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º³õÖÐÊýѧ À´Ô´£º ÌâÐÍ£ºÑ¡ÔñÌâ
| A£® | a£¾0£¬b£¾0 | B£® | a£¼0£¬b£¼0 | ||
| C£® | a¡¢bÒìºÅÇÒÕýÊýµÄ¾ø¶ÔÖµ½ÏС | D£® | a¡¢bÒìºÅÇÒ¸ºÊýµÄ¾ø¶ÔÖµ½ÏС |
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º³õÖÐÊýѧ À´Ô´£º ÌâÐÍ£ºÌî¿ÕÌâ
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º³õÖÐÊýѧ À´Ô´£º ÌâÐÍ£º½â´ðÌâ
 Èç¹ûÓÐÀíÊýa¡¢b¡¢cÔÚÊýÖáÉϵÄλÖÃÈçͼËùʾ£¬
Èç¹ûÓÐÀíÊýa¡¢b¡¢cÔÚÊýÖáÉϵÄλÖÃÈçͼËùʾ£¬²é¿´´ð°¸ºÍ½âÎö>>
¹ú¼ÊѧУÓÅÑ¡ - Á·Ï°²áÁбí - ÊÔÌâÁбí
ºþ±±Ê¡»¥ÁªÍøÎ¥·¨ºÍ²»Á¼ÐÅÏ¢¾Ù±¨Æ½Ì¨ | ÍøÉÏÓк¦ÐÅÏ¢¾Ù±¨×¨Çø | µçÐÅթƾٱ¨×¨Çø | ÉæÀúÊ·ÐéÎÞÖ÷ÒåÓк¦ÐÅÏ¢¾Ù±¨×¨Çø | ÉæÆóÇÖȨ¾Ù±¨×¨Çø
Î¥·¨ºÍ²»Á¼ÐÅÏ¢¾Ù±¨µç»°£º027-86699610 ¾Ù±¨ÓÊÏ䣺58377363@163.com