48°
分析:延长BA到F,使AF=AC,由AB+AC=BE,等量代换可得出AB+AF=BE,而BA+AF=BF,可得出BF=BE,即三角形BEF为等腰三角形,用顶角∠B,利用三角形的内角和定理表示出底角∠F,再由AD与AE垂直,得到∠DAE为直角,又∠BAD=∠DAC=9°,根据平角的定义求出∠FAE=81°,同时由∠DAC=9°,由直角∠DAE-∠DAC求出∠CAE也为81°,可得出∠CAE=∠FAE,再由AF=AC,AE为公共边,利用SAS可得出三角形AFE与三角形ACE全等,根据全等三角形的对应角相等可得出∠F=∠ACE,由∠ACE为三角形ABC的外角,根据外角的性质得到∠ACE=∠B+∠BAC,由∠BAC的度数,表示出∠ACE,即为∠F,根据表示出的∠F相等列出关于∠B的方程,求出方程的解即可得到∠B的度数.
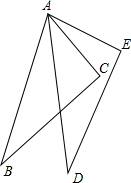
解答:延长BA到F,使AF=AC,连接EF,如图所示:

∵AB+AC=BE,
∴AB+AF=BE,即BF=BE,
∴∠F=∠BEF=
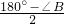
,
∵∠BAD=∠DAC=9°,AD⊥AE,即∠DAE=90°,
∴∠FAE=180°-(∠BAD+∠DAE)=180°-(9°+90°)=81°,
∠CAE=∠DAE-∠DAC=90°-9°=81°,
∴∠FAE=∠CAE,
在△AFE和△ACE中,
∵
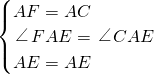
,
∴△AFE≌△ACE(SAS),
∴∠F=∠ACE,
又∵∠ACE为△ABC的外角,
∴∠ACE=∠B+∠BAC=∠B+18°,
∴∠F=∠B+18°,
∴∠B+18°=
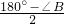
,
则∠B=48°.
故答案为:48°
点评:此题考查了等腰三角形的判定与性质,全等三角形的判定与性质,三角形的外角性质,以及三角形的内角和定理,利用了转化及等量代换的思想,其中根据题意作出如图所示的辅助线是解本题的关键.

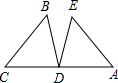
 如图:已知∠BAD=∠DAC=9°,AD⊥AE,且AB+AC=BE.则∠B=________.
如图:已知∠BAD=∠DAC=9°,AD⊥AE,且AB+AC=BE.则∠B=________.
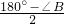 ,
,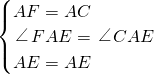 ,
,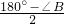 ,
,

 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案