
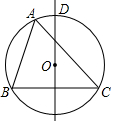
 如图,⊙O是△ABC的外接圆,BC的中垂线与$\widehat{AC}$相交于D点,若∠B=74°,∠C=46°,则$\widehat{AD}$的度数为( )
如图,⊙O是△ABC的外接圆,BC的中垂线与$\widehat{AC}$相交于D点,若∠B=74°,∠C=46°,则$\widehat{AD}$的度数为( )| A. | 23° | B. | 28° | C. | 30° | D. | 37° |
分析 首先连接OB,OC,AO,设DO交BC于点E,由∠B=74°,∠C=46°,即可求得∠BAC的度数,又由△ABC的边BC的垂直平分线与△ABC的外接圆相交于点D,根据圆周角定理,即可求得∠AOB与∠BOE的度数,继而求得答案.
解答 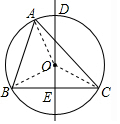 解:如图,连接OB,OC,AO,设DO交BC于点E,
解:如图,连接OB,OC,AO,设DO交BC于点E,
∵OD是△ABC的边BC的垂直平分线,
∴∠BOE=$\frac{1}{2}$∠BOC,
∵∠BAC=$\frac{1}{2}$∠BOC,
∴∠BOE=∠BAC,
∵∠ABC=74°,∠ACB=46°,
∴∠BOE=∠BAC=180°-∠ABC-∠ACB=60°,
∴∠BOD=180°-∠BOE=180°-60°=120°,
∵∠AOB=2∠ACB=92°,∴$\widehat{AB}$的度数为:92°,
∴$\widehat{AD}$的度数为:120°-92°=28°.
故选:B.
点评 此题考查了圆周角定理以及线段垂直平分线的性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:选择题
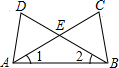 如图,∠1=∠2,∠C=∠D,AC、BD交于E点,下列结论中正确的有( )
如图,∠1=∠2,∠C=∠D,AC、BD交于E点,下列结论中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
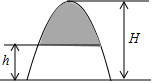 如图所示的图形,是由开口向下的抛物线两边平齐的一部分和一水平线段围成的,设其总高度为H,空白部分的高度是h(0≤h≤H),阴影部分的面积是S,则S随h变化的大致趋势是( )
如图所示的图形,是由开口向下的抛物线两边平齐的一部分和一水平线段围成的,设其总高度为H,空白部分的高度是h(0≤h≤H),阴影部分的面积是S,则S随h变化的大致趋势是( )| A. | 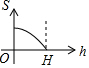 | B. | 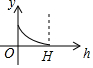 | C. | 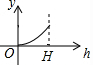 | D. | 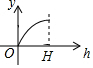 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{9}$ | C. | $\frac{1}{18}$ | D. | $\frac{1}{36}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | $-\frac{3}{2}$ | D. | $-\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
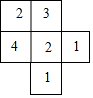 如图,是一个由小正方体搭成的几何体的俯视图,小正方形中的数字表示在该位置的正方体的个数.请你画出从正面看和从上面看到的图形(要用直尺画).
如图,是一个由小正方体搭成的几何体的俯视图,小正方形中的数字表示在该位置的正方体的个数.请你画出从正面看和从上面看到的图形(要用直尺画).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com