
分析 从0,1,2三个数中任取的一个数,从0,2个数中任取的一个数则共有种结果,且每种结果出现的机会相同,关于x的一元二次方程x2-2mx+n=0有实数根的条件是△=4m2-4n≥0,在上面得到的数对中验证得出答案即可.
解答 解:从0,1,2三个数中任取的一个数,从0,2三个数中任取的一个数则共有:3×2=6种结果为(0,0)、(1,0)、(2,0)、(0,2)、(1,2)、(2,2),
∵满足关于x的一元二次方程x2-2mx+n=0有实数根,则△=(-2m)2-4n=4m2-4n≥0,符合的有(0,0)、(1,0)、(2,0)、(2,2),4个,
∴关于x的一元二次方程x2-2mx+n=0有实数根的概率为$\frac{2}{3}$.
故答案为:$\frac{2}{3}$.
点评 本题是概率与一元二次方程的根的判别式相结合的题目.正确理解列举法求概率的条件以及一元二次方程有根的条件是关键.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
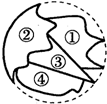 一圆形玻璃被打碎后,其中四块碎片如图所示,若选择其中一块碎片带到商店,配制与原来大小一样的圆形玻璃,选择的是( )
一圆形玻璃被打碎后,其中四块碎片如图所示,若选择其中一块碎片带到商店,配制与原来大小一样的圆形玻璃,选择的是( )| A. | ① | B. | ③ | C. | ② | D. | ④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 a、b、c在数轴上的位置如图所示,则:
a、b、c在数轴上的位置如图所示,则:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
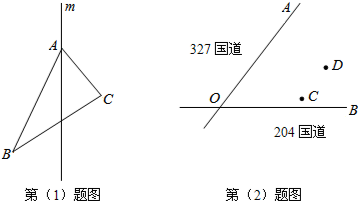
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com