
分析 (1)把(1,b)代入y=2x-3求得b=-1,再代入y=ax2即可求得a;
(2)根据解析式y=-x2即可求得顶点坐标和对称轴;
(3)根据二次函数y=ax2的性质求得即可;
(4)先求得交点坐标,根据三角形的面积公式求得即可.
解答 解:(1)∵直线y=2x-3经过(1,b).
∴b=2-3=-1,
∴函数y=ax2(a≠0)与直线y=2x-3交于(1,-1).
把(1,-1)代入y=ax2(a≠0)得,a=-1;
(2)∵a=-1,
∴抛物线为y=-x2,
∴抛物线的顶点为(0,0),对称轴是y轴;
(3)∵a=-1<0,开口向下,
∴在对称轴的左侧y随x的增大而增大,
∴x<0时,二次函数y=ax2中y随x的增大而增大;
(4)把y=-2代入y=-x2得,-2=-x2,
∴x=±$\sqrt{2}$,
∴S=$\frac{1}{2}$×2$\sqrt{2}$×2=2$\sqrt{2}$.
点评 本题考查了待定系数法求二次函数的解析式以及二次函数的性质和二次函数图象上点的坐标特征,熟练掌握待定系数法和二次函数的性质是解题的关键.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{7}{3}$<-2 | B. | -$\frac{3}{4}$<-$\frac{4}{5}$ | C. | |-5|<|-5$\frac{1}{2}$| | D. | 1.7>-1.7 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
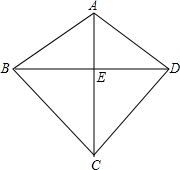 如图,平面上的四边形ABCD是一只“风筝”的骨架,其中AB=AD,CB=CD,某同学观察了这只“风筝”的骨架后,认为四边形ABCD的两条对角线AC,BD垂直,垂足为E,并且BE=ED,你同意这位同学的判断吗?请说明理由.
如图,平面上的四边形ABCD是一只“风筝”的骨架,其中AB=AD,CB=CD,某同学观察了这只“风筝”的骨架后,认为四边形ABCD的两条对角线AC,BD垂直,垂足为E,并且BE=ED,你同意这位同学的判断吗?请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com