练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    菱形ABCD的边长是5，两条对角线交于O点，且AO，BO的长分别等于关于x的方程x2＋(2m－1)x＋m2＋3＝0的两根，则m的值是

    [　　]

    A．－3
    B．5
    C．5或－3
    D．－5或3
    答案：A
    解析：

    由根与系数的关系AO＋BO＝－(2m－1)…①，AO·BO＝m2＋3…②，又菱形对角线互相垂直平分，

    　　∴AO2＋BO2＝(AO＋BO)2－2AO·BO＝52，将①，②代入上式即可得出 ：(2m－1)2－2×（m2＋3）=25

        ∴m1＝－3，m2＝5，又AO＋BO＞0，

    　　∴m＝5必须舍去，故m＝－3．


    提示：

    　　由根与系数的关系AO＋BO＝－(2m－1)…①，AO·BO＝3…②，又菱形对角线互相垂直平分，

    　　∴AO2＋BO2＝(AO＋BO)2－2AO·BO＝52，将①，②代入上式即可得出m1＝－3，m2＝5，又AO＋BO＞0，

    　　∴m＝5必须舍去，故m＝－3．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    己知菱形ABCD的边长是6，点E在直线AD上，DE=3，连接BE与对角线AC相交于点M，则
    MCAM
    的值是
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    1、如图，在菱形ABCD中，∠A=60°，E、F分别是AB、AD的中点，若EF=2，则菱形ABCD的边长是
    4
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知菱形ABCD的边长是8，点E在直线AD上，若DE=3，连接BE与对角线AC相交于点M，则
    MCAM
    的值是
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

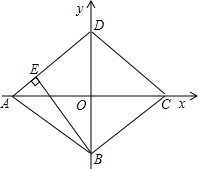    已知：直角坐标系中菱形ABCD的位置如图，C，D两点的坐标分别为（4，0），（0，3）．现有两动点P，Q分别从A，C同时出发，点P沿线段AD向终点D运动，点Q沿折线CBA向终点A运动，设运动时间为t秒．
    （1）填空：菱形ABCD的边长是
    5
    5
    、面积是
    24
    24
    、高BE的长是
    24
    5
    24
    5
    ；
    （2）若点P的速度为每秒1个单位，点Q的速度为每秒2个单位．当点Q在线段BA上时，求△APQ的面积S关于t的函数关系式；
    （3）若点P的速度为每秒1个单位，点Q的速度变为每秒k个单位，求出当t=4秒时，△APQ为等腰三角形时k的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

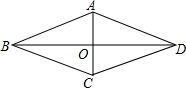    （2012•南京二模）如图，菱形ABCD的边长是13，点O是两条对角线的交点，且OB=12．约定：三角形三边上的任意一点到圆上的任意一点距离的最小值叫做三角形与圆的距离．依据这个约定，可知当⊙C的半径是
    2或16
    2或16
    时，△ABD与⊙C的距离为3．

    查看答案和解析>>

    同步练习册答案