练习册

  • 练习册
  • 试题
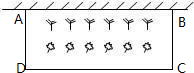    精英家教网 > 初中数学 > 题目详情
    如图所示，一边靠学校院墙，其他三边用40 m长的篱笆围成一个矩形花圃，设矩形ABCD的边AB =x m，面积为Sm2
    (1)写出S与x之间的函数关系式，并求当S=200 m2时，x的值；
    (2)设矩形的边BC=y m，如果x，y满足关系式x：y=y：(x+y)，即矩形成黄金矩形，求此黄金矩形的长和宽．
    解：(l)S=x(40- 2x)=-2 x2+40x,  当S=200时，.  
    (2)当BC=y，则y=40-2x
    ①又y2 =x(x+y)  ②由①、②
    解得x=20±，其中20+不合题意，舍去，
    x=20-，y=  
    当矩形成黄金矩形时，宽为20-m，长为m.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    精英家教网学校要在一块一边靠墙（墙长15m）的空地上修建一个矩形花园ABCD，花园的一边靠墙，另三边用总长为40m的栅栏围成（如图所示）．若设花园的BC边长为x（m），花园的面积为y（m2）．
    （1）求y与x之间的函数关系式，并写出自变量x的取值范围；
    （2）满足条件的花园面积能达到200m2吗？若能，求出此时x的值；若不能，说明理由；
    （3）当x取何值时，花园的面积最大？最大面积为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

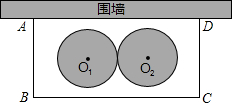    精英家教网某学校要在围墙旁建一个长方形的中药材种植实习苗圃，苗圃的一边靠围墙（墙的长度不限），另三边用木栏围成，建成的苗圃为如图所示的长方形ABCD．已知木栏总长为120米，设AB边的长为x米，长方形ABCD的面积为S平方米．
    （1）求S与x之间的函数关系式（不要求写出自变量x的取值范围）．当x为何值时，S取得最值（请指出是最大值还是最小值）？并求出这个最值；
    （2）学校计划将苗圃内药材种植区域设计为如图所示的两个相外切的等圆，其圆心分别为O1和O2，且O1到AB、BC、AD的距离与O2到CD、BC、AD的距离都相等，并要求在苗圃内药材种植区域外四周至少要留够0.5米宽的平直路面，以方便同学们参观学习．当（l）中S取得最值时，请问这个设计是否可行？若可行，求出圆的半径；若不可行，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

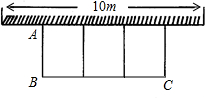    如图所示，某学校要建一个中间有两道篱笆隔断的长方形花圃，花圃的一边靠墙精英家教网（墙的最大可利用长度为10m），现有篱笆长24m．设花圃的宽AB为xm，面积为Sm2．
    （1）求S与x之间的函数关系式；
    （2）如果要围成面积为32m2的花圃，AB的长是多少米？
    （3）能围成面积比32m2更大的花圃吗？如果能，请求出最大面积，并给出设计方案；如果不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：新教材完全解读　九年级数学　(下册)　(配华东师大版新课标) 华东师大版新课标 题型：044

    如图所示，一边靠学校院墙，其他三边用40 m长的篱笆围成一个矩形花圃，设矩形ABCD的边AB为x m，面积为S m2．

    (1)求S与x之间的函数关系式，并求当S＝200 m2时，x的值；

    (2)设矩形的边BC为y m，如果x，y满足关系式x∶y＝y∶(x＋y)，则矩形即为黄金矩形，求这个黄金矩形的长和宽．

    查看答案和解析>>

    同步练习册答案