
 如图,在△ABC中,AB=AC=2,∠B=40°,点D在线段AB上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线AC段于E.
如图,在△ABC中,AB=AC=2,∠B=40°,点D在线段AB上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线AC段于E.分析 (1)利用邻补角的性质和三角形内角和定理解题;
(2)当DC=2时,利用∠DEC+∠EDC=140°,∠ADB+∠EDC=140°,求出∠ADB=∠DEC,再利用AB=DC=2,即可得出△ABD≌△DCE.
(3)当∠BDA的度数为110°或80°时,△ADE的形状是等腰三角形.
解答 解:(1)∵在△BAD中,∠B=∠C=∠40°,∠BDA=115°,
∴∠BAD=180°-∠B-∠BDA=180°-40°-115°=25°;
∠EDC=180°-∠ADB-∠ADE=180°-115°-40°=25°.
∠DEC=180°-∠C-∠EDC=180°-40°-25°=115°,
故答案为:25,115;
(2)当DC=2时,△ABD≌△DCE,理由如下:
∵∠C=40°,
∴∠DEC+∠EDC=140°,
又∵∠ADE=40°,
∴∠ADB+∠EDC=140°,
∴∠ADB=∠DEC,
又∵AB=DC=2,
在△ABD和△DCE中,$\left\{\begin{array}{l}{∠ADB=∠DEC}&{\;}\\{∠B=∠C}&{\;}\\{AB=DC}&{\;}\end{array}\right.$,
∴△ABD≌△DCE(AAS);
(3)可以;当∠BDA的度数为110°或80°时,△ADE的形状是等腰三角形,
∵∠BDA=110°时,
∴∠ADC=70°,
∵∠C=40°,
∴∠DAE=70°,
∴∠AED=180°-70°-40°=70°
∴△ADE的形状是等腰三角形;
∵当∠BDA的度数为80°时,
∴∠ADC=100°,
∵∠C=40°,
∴∠DAE=40°,
∴∠DAE=∠ADE
∴△ADE的形状是等腰三角形.
点评 此题主要考查学生对等腰三角形的判定与性质,全等三角形的判定与性质,三角形外角的性质等知识点的理解和掌握,此题涉及到的知识点较多,综合性较强.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
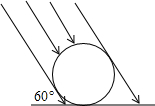 如图,太阳光线与地面成60°的角,照在地面的一只排球上,排球在地面的投影长是14$\sqrt{3}$cm,则排球的直径是( )
如图,太阳光线与地面成60°的角,照在地面的一只排球上,排球在地面的投影长是14$\sqrt{3}$cm,则排球的直径是( )| A. | 7cm | B. | 14cm | C. | 21cm | D. | 21$\sqrt{3}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 经过有交通信号灯的路口,遇到红灯是随机事件 | |
| B. | 某妇产医院里,下一个出生的婴儿是女孩是必然事件 | |
| C. | 357人中至少有2人生日(公历)相同是确定事件 | |
| D. | 长分别为3,5,9厘米的三条线段不能围成一个三角形是确定事件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com