

ЗжЮі ЃЈ1ЃЉАбAЁЂCСНЕузјБъДњШыХзЮяЯпНтЮіЪНПЩЧѓЕУaЁЂcЕФжЕЃЌПЩЧѓЕУХзЮяЯпНтЮіЃЛ
ЃЈ2ЃЉПЩЧѓЕУЕуCЙигкxжсЕФЖдГЦЕуCЁфЕФзјБъЃЌСЌНгCЁфNНЛxжсгкЕуKЃЌдйЧѓЕУжБЯпCЁфKЕФНтЮіЪНЃЌПЩЧѓЕУKЕузјБъЃЛ
ЃЈ3ЃЉЙ§ЕуEзїEGЁЭxжсгкЕуGЃЌЩшQЃЈmЃЌ0ЃЉЃЌПЩБэЪОГіABЁЂBQЃЌдйжЄУїЁїBQEЁеЁїBACЃЌПЩБэЪОГіEGЃЌПЩЕУГіЁїCQEЙигкmЕФНтЮіЪНЃЌдйИљОнЖўДЮКЏЪ§ЕФаджЪПЩЧѓЕУQЕуЕФзјБъЃЛ
ЃЈ4ЃЉЗжDO=DFЁЂFO=FDКЭOD=OFШ§жжЧщПіЃЌЗжБ№ИљОнЕШбќШ§НЧаЮЕФаджЪЧѓЕУFЕуЕФзјБъЃЌНјвЛВНЧѓЕУPЕузјБъМДПЩЃЎ
НтД№ НтЃК
ЃЈ1ЃЉЁпХзЮяЯпОЙ§ЕуCЃЈ0ЃЌ4ЃЉЃЌAЃЈ4ЃЌ0ЃЉЃЌ
Ёр$\left\{\begin{array}{l}{c=4}\\{16a-8a+4=0}\end{array}\right.$ЃЌНтЕУ$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{c=4}\end{array}\right.$ЃЌ
ЁрХзЮяЯпНтЮіЪНЮЊy=-$\frac{1}{2}{x^2}+x+4$ЃЛ
ЃЈ2ЃЉгЩЃЈ1ЃЉПЩЧѓЕУХзЮяЯпЖЅЕуЮЊNЃЈ1ЃЌ$\frac{9}{2}$ЃЉЃЌ
ШчЭМ1ЃЌзїЕуCЙигкxжсЕФЖдГЦЕуCЁфЃЈ0ЃЌ-4ЃЉЃЌСЌНгCЁфNНЛxжсгкЕуKЃЌдђKЕуМДЮЊЫљЧѓЃЌ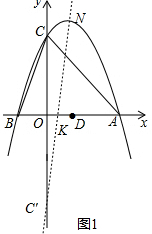
ЩшжБЯпCЁфNЕФНтЮіЪНЮЊy=kx+bЃЌАбCЁфЁЂNЕузјБъДњШыПЩЕУ$\left\{\begin{array}{l}{k+b=\frac{9}{2}}\\{b=-4}\end{array}\right.$ЃЌНтЕУ$\left\{\begin{array}{l}{k=\frac{17}{2}}\\{b=-4}\end{array}\right.$ЃЌ
ЁржБЯпCЁфNЕФНтЮіЪНЮЊy=$\frac{17}{2}x-4$ЃЌ
Сюy=0ЃЌНтЕУx=$\frac{8}{17}$ЃЌ
ЁрЕуKЕФзјБъЮЊЃЈ$\frac{8}{17}$ЃЌ0ЃЉЃЛ
ЃЈ3ЃЉЩшЕуQЃЈmЃЌ0ЃЉЃЌЙ§ЕуEзїEGЁЭxжсгкЕуGЃЌШчЭМ2ЃЌ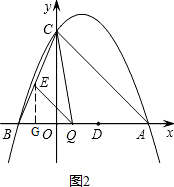
гЩ-$\frac{1}{2}{x^2}+x+4$=0ЃЌЕУx1=-2ЃЌx2=4ЃЌ
ЁрЕуBЕФзјБъЮЊЃЈ-2ЃЌ0ЃЉЃЌAB=6ЃЌBQ=m+2ЃЌ
гжЁпQEЁЮACЃЌ
ЁрЁїBQEЁеЁїBACЃЌ
Ёр$\frac{EG}{CO}=\frac{BQ}{BA}$ЃЌМД$\frac{EG}{4}=\frac{m+2}{6}$ЃЌНтЕУEG=$\frac{2m+4}{3}$ЃЛ
ЁрSЁїCQE=SЁїCBQ-SЁїEBQ=$\frac{1}{2}ЃЈCO-EGЃЉ•BQ$=$\frac{1}{2}ЃЈm+2ЃЉЃЈ4-\frac{2m+4}{3}ЃЉ=-\frac{1}{3}{m^2}+\frac{2}{3}m+\frac{8}{3}$=$-\frac{1}{3}{ЃЈm-1ЃЉ^2}+3$ЃЎ
гжЁп-2ЁмmЁм4ЃЌ
ЁрЕБm=1ЪБЃЌSЁїCQEгазюДѓжЕ3ЃЌДЫЪБQЃЈ1ЃЌ0ЃЉЃЛ
ЃЈ4ЃЉДцдкЃЎдкЁїODFжаЃЌ
ЃЈЂЁЃЉШєDO=DFЃЌЁпAЃЈ4ЃЌ0ЃЉЃЌDЃЈ2ЃЌ0ЃЉЃЌ
ЁрAD=OD=DF=2ЃЎ
гждкRtЁїAOCжаЃЌOA=OC=4ЃЌ
ЁрЁЯOAC=45ЁуЃЎ
ЁрЁЯDFA=ЁЯOAC=45ЁуЃЎ
ЁрЁЯADF=90ЁуЃЎ
ДЫЪБЃЌЕуFЕФзјБъЮЊЃЈ2ЃЌ2ЃЉЃЎ
гЩ-$\frac{1}{2}{x^2}+x+4$=2ЃЌЕУx1=1+$\sqrt{5}$ЃЌx2=1-$\sqrt{5}$ЃЎ
ДЫЪБЃЌЕуPЕФзјБъЮЊЃКP1ЃЈ1+$\sqrt{5}$ЃЌ2ЃЉЛђP2ЃЈ1-$\sqrt{5}$ЃЌ2ЃЉЃЛ
ЃЈЂЂЃЉШєFO=FDЃЌЙ§ЕуFзїFMЁЭxжсгкЕуMЃЎ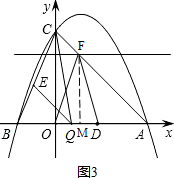
гЩЕШбќШ§НЧаЮЕФаджЪЕУЃКOM=$\frac{1}{2}$OD=1ЃЌ
ЁрAM=3ЃЎ
ЁрдкЕШбќжБНЧЁїAMFжаЃЌMF=AM=3ЃЎ
ЁрFЃЈ1ЃЌ3ЃЉЃЎ
гЩ-$\frac{1}{2}{x^2}+x+4$=3ЃЌЕУx1=1+$\sqrt{3}$ЃЌx2=1-$\sqrt{3}$ЃЎ
ДЫЪБЃЌЕуPЕФзјБъЮЊЃКP3ЃЈ1+$\sqrt{3}$ЃЌ3ЃЉЛђP4ЃЈ1-$\sqrt{3}$ЃЌ3ЃЉЃЛ
ЃЈЂЃЃЉШєOD=OFЃЌ
ЁпOA=OC=4ЃЌЧвЁЯAOC=90ЁуЃЎ
ЁрAC=4$\sqrt{2}$ЃЎ
ЁрЕуOЕНACЕФОрРыЮЊ2$\sqrt{2}$ЃЎ
ЖјOF=OD=2ЃМ2$\sqrt{2}$ЃЌгыOFЁн2$\sqrt{2}$УЌЖмЃЎ
ЁрдкACЩЯВЛДцдкЕуЪЙЕУOF=OD=2ЃЎ
ДЫЪБЃЌВЛДцдкетбљЕФжБЯпlЃЌЪЙЕУЁїODFЪЧЕШбќШ§НЧаЮЃЎ
злЩЯЫљЪіЃЌДцдкетбљЕФжБЯпlЃЌЪЙЕУЁїODFЪЧЕШбќШ§НЧаЮЃЎЫљЧѓЕуPЕФзјБъЮЊЃКЃЈ1+$\sqrt{5}$ЃЌ2ЃЉЛђЃЈ1-$\sqrt{5}$ЃЌ2ЃЉЛђЃЈ1+$\sqrt{3}$ЃЌ3ЃЉЛђЃЈ1-$\sqrt{3}$ЃЌ3ЃЉЃЎ
ЕуЦР БОЬтжївЊПМВщЖўДЮКЏЪ§ЕФзлКЯгІгУЃЌЩцМАД§ЖЈЯЕЪ§ЗЈЁЂжсЖдГЦЕФгІгУЁЂЯрЫЦШ§НЧаЮЕФХаЖЈКЭаджЪЁЂЕШбќжБНЧШ§НЧаЮЕФаджЪЕШжЊЪЖЕуЃЎдкЃЈ1ЃЉжазЂвтД§ЖЈЯЕЪ§ЗЈЕФВНжшЃЌдкЃЈ2ЃЉжаШЗЖЈГіKЕФЮЛжУЪЧНтЬтЕФЙиМќЃЌдкЃЈ3ЃЉжагУQЕуЕФзјБъБэЪОГіEGЕФГЄЪЧНтЬтЕФЙиМќЃЌдкЃЈ4ЃЉжаЗжШ§жжЧщПіЗжБ№ЧѓЕУFЕуЕФзјБъЪЧНтЬтЕФЙиМќЃЎБОЬтПМВщжЊЪЖЕуНЯЖрЃЌзлКЯадКмЧПЃЌФбЖШНЯДѓЃЎ


 ПкЫуЬтПЈМггІгУЬтМЏбЕЯЕСаД№АИ
ПкЫуЬтПЈМггІгУЬтМЏбЕЯЕСаД№АИ злКЯздВтЯЕСаД№АИ
злКЯздВтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | СНЕуШЗЖЈвЛЬѕжБЯп | BЃЎ | СНЕужЎМфЯпЖЮзюЖЬ | ||
| CЃЎ | ДЙЯпЖЮзюЖЬ | DЃЎ | Ш§НЧаЮСНБпжЎКЭДѓгкЕкШ§Бп |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
 ШчЭМЃЌжмГЄЮЊ16ЕФСтаЮABCDжаЃЌЕуEЃЌFЗжБ№дкABЃЌADБпЩЯЃЌAE=1ЃЌAF=3ЃЌPЮЊBDЩЯвЛЖЏЕуЃЌдђЯпЖЮEP+FPЕФГЄзюЖЬЮЊЃЈЁЁЁЁЃЉ
ШчЭМЃЌжмГЄЮЊ16ЕФСтаЮABCDжаЃЌЕуEЃЌFЗжБ№дкABЃЌADБпЩЯЃЌAE=1ЃЌAF=3ЃЌPЮЊBDЩЯвЛЖЏЕуЃЌдђЯпЖЮEP+FPЕФГЄзюЖЬЮЊЃЈЁЁЁЁЃЉ| AЃЎ | 3 | BЃЎ | 4 | CЃЎ | 5 | DЃЎ | 6 |
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com