
【题目】如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB,CD交于点E,F,连结BF,交AC于点M,连结DE,BO.若∠BOC=60°,FO=FC,则下列结论:①AE=CF;②BF垂直平分线段OC;③△EOB≌△CMB;④四边形是BFDE菱形.其中正确结论的个数是( )

A.1个B.2个C.3个D.4个
【答案】C
【解析】
利用ASA定理证明△AOE≌△COF,从而判断①;利用线段垂直平分线的性质的逆定理可得结论②;在△EOB和△CMB中,对应直角边不相等,则两三角形不全等,从而判断③;连接BD,先证得BO=DO, OE=OF,进而证得OB⊥EF,因为BD、EF互相垂直平分,即可证得四边形EBFD是菱形,从而判断④.
解:∵矩形ABCD中,O为AC中点
∴∠DCA=∠BAC,OA=OC,∠AOE=∠COF
∴△AOE≌△COF
∴AE=CF,故①正确
∵矩形ABCD中,O为AC中点,
∴OB=OC,
∵∠COB=60°,
∴△OBC是等边三角形,
∴OB=BC,
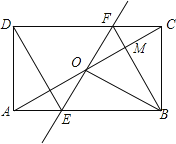
∵FO=FC,
∴FB垂直平分OC,故②正确;
∵△BOC为等边三角形,FO=FC,
∴BO⊥EF,BF⊥OC,
∴∠CMB=∠EOB=90°,
∴BO≠BM,
∴△EOB与△CMB不全等;故③错误;
连接BD,
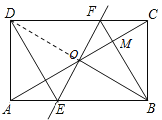
∵四边形ABCD是矩形,
∴AC=BD,AC、BD互相平分,
∵O为AC中点,
∴BD也过O点,且BO=DO
由①可知△AOE≌△COF,∴OE=OF
∴四边形EBFD是平行四边形
由②可知,OB=CB,OF=FC
又∵BF=BF
∴△OBF≌△OCF
∴BD⊥EF
∴平行四边形EBFD是菱形,故④正确
所以其中正确结论的个数为3个;
故选:C.


科目:初中数学 来源: 题型:
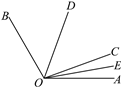
【题目】已知∠AOC和∠BOC,OD平分∠BOC,OE平分∠AOC.
(1)请写出一对相等的角;
(2)若∠AOC在∠BOC的外部,且∠AOB=120°,如图,其他条件不变,求∠EOD的度数.从结果你能看出∠EOD与∠AOB有什么数量关系吗?
(3)若∠AOC=α,∠BOC=β(α,β都大于0°且小于180°,且α<β),其他条件不变,试求∠EOD的度数(结果用含α,β的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架,书中的算法体系至今仍在推动着计算机的发展和应用.《九章算术》中记载:今有户不知高、广,竿不知长、短.横之不出四尺,从之不出二尺,邪之适出.问户高、广、邪各几何?译文是:今有门不知其高、宽,有竿,不知其长、短,横放,竿比门宽长出![]() 尺;竖放,竿比门高长出
尺;竖放,竿比门高长出![]() 尺;斜放,竿与门对角线恰好相等.问门高、宽、对角线长分别是多少?若设门对角线长为
尺;斜放,竿与门对角线恰好相等.问门高、宽、对角线长分别是多少?若设门对角线长为![]() 尺,则可列方程为__________.
尺,则可列方程为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,以
,以![]() 为圆心,任意长为半径画弧分别交
为圆心,任意长为半径画弧分别交![]() 、
、![]() 于点
于点![]() 和
和![]() ,再分别以
,再分别以![]() 、
、![]() 为圆心,大于
为圆心,大于![]() 的长为半径画弧,两弧交于点
的长为半径画弧,两弧交于点![]() ,连结
,连结![]() 并延长交
并延长交![]() 于点
于点![]() ,则下列说法中正确的个数是( )
,则下列说法中正确的个数是( )
①![]() 是
是![]() 的平分线;②
的平分线;②![]() ;③点
;③点![]() 在
在![]() 的垂直平分线上;④
的垂直平分线上;④![]()
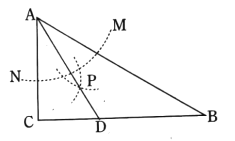
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象经过A(-1,0)、B(4,5)三点.
的图象经过A(-1,0)、B(4,5)三点.
(1)求此二次函数的解析式;
(2)当x为何值时,y随x的增大而减小?
(3)当x为何值时,y>0?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2-3x+m(m为常数)的图象与x轴的一个交点为(1,0),则关于x的一元二次方程x2-3x+m=0的两实数根是( )
A. x1=1,x2=-1 B. x1=1,x2=2 C. x1=1,x2=0 D. x1=1,x2=3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于关于x的二次函数y=x2-2mx-3,有下列说法:① 它的图象与x轴有两个公共点; ② 如果当x≤1时y随x的增大而减小,则m=1; ③ 如果将它的图象向左平移3个单位后过原点,则m=-1; ④ 如果当x=5时的函数值与x=2012时的函数值相等,则当x=2017时的函数值为-3.其中正确的说法有______.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() 为直线
为直线![]() 上一点,
上一点,![]() 为直线
为直线![]() 上一点,
上一点,![]() ,设
,设![]() ,
,![]() .
.
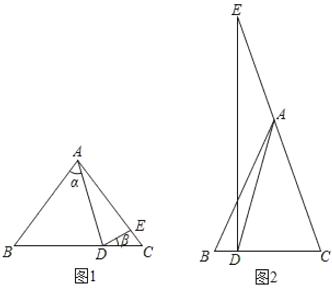
(1)如图1,若点![]() 在线段
在线段![]() 上,点
上,点![]() 在线段
在线段![]() 上,则
上,则![]() ,
,![]() 之间关系式为__________.
之间关系式为__________.
(2)如图2,若点![]() 在线段
在线段![]() 上,点
上,点![]() 在
在![]() 延长线上,则
延长线上,则![]() ,
,![]() 之间关系式为__________.
之间关系式为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com