练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    6．方程x2-ax+4=0的两根相等，则a=（　　）
    A．2B．±4C．-4D．4

    分析 判断上述方程的根的情况，只要看根的判别式△=b2-4ac的值的符号就可以了．有两个相等实数根的一元二次方程就是判别式的值是0，由此建立关于a的方程解答即可．

    解答 解：∵方程x2-ax+4=0的两根相等，
    ∴（-a）2-4×1×4=0，
    解得：a=±4．
    故选：B．

    点评 此题考查一元二次方程根的情况与判别式△的关系：（1）△＞0?方程有两个不相等的实数根；（2）△=0?方程有两个相等的实数根；（3）△＜0?方程没有实数根．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

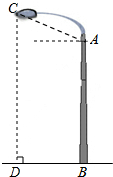    16．如图，某广场有一灯柱AB高7.5米，灯的顶端C离灯柱顶端A的距离CA为1.7米，且∠CAB=110°，求灯的顶端C距离地面的高度CD．（结果精确到0.1米）
    【参考数据：sin20°=0.34，cos20°=0.94，tan20°=0.36】

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．推理填空：
    如图：①若∠1=∠2，
    则DC∥AB（内错角相等，两直线平行　）
    ②若∠DAB+∠ABC=180°，
    则AD∥BC（同旁内角互补，两直线平行　）
    ③当DC∥AB时，
    ∠3=∠A （两直线平行，同位角相等　）
    ④当DC∥AB时，∠C+∠ABC=180°（两直线平行，同旁内角互补 ）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．不等式组$\left\{\begin{array}{l}{2x＞-1}\\{-3x+9≥0}\end{array}\right.$有（　　）个整数解．
    A．2B．3C．4D．5

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

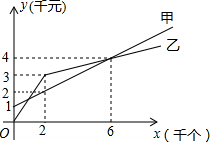    1．某单位准备印制一批证书，现有两个印刷厂可供选择，甲厂费用分为制版费和印刷费两部分先收取固定的制版费，再按印刷数量收取印刷费，乙厂直接按印刷数量收取印刷费．甲厂的总费用y1（干元）、乙厂的总费用y2（千元）与印制证书数量x（千个）的函数关系图分别如图中甲、乙所示．
    （l）甲厂的制版费为1千元，印刷费为平均每个0.5元，甲厂的费用yl与证书数量x之间的函数关系式为yl=0.5x+1；
    （2）当印制证书数量不超过2千个时，乙厂的印刷费为平均每个1.5　元；当印制证书数量超过2千个时，求乙厂的总费用y2与证书数量x之间的函数关系式为y2=$\frac{1}{4}x+\frac{5}{2}$；
    （3）若甲厂的总费用高于乙厂，但相差不超过500元，该单位需印制证书数量的范围是6＜x≤8或0.5≤x＜1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．在围棋盒中有x枚白棋子和y枚黑棋子，从盒中随机取出一枚棋子，取得白棋子的概率是$\frac{3}{5}$；如果再往盒中放入6枚黑棋子，从盒中随机取出一枚棋子，取得的是白棋子的概率是$\frac{1}{2}$．则原来盒中有白棋子18枚．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    18．多项式2x2-5x+4的一次项系数是-5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．如果$\frac{3（2a-1）}{5（2a-1）}=\frac{3}{5}$成立，则a的取值范围是a≠$\frac{1}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．计算：|-3|+（-1）2014+（2-$\sqrt{3}$）0=5．

    查看答案和解析>>

    同步练习册答案