
 推理填空:
推理填空:分析 ①根据平行线的判定内错角相等,两直线平行即可得到结论;
②根据平行线的判定同旁内角互补,两直线平行即可得到结论;
③根据平行线的性质两直线平行,同位角相等即可得到结论;
④根据平行线的性质两直线平行,同旁内角互补即可得到结论.
解答 解:①∵∠1=∠2,
∴DC∥AB(内错角相等,两直线平行),
故答案为:DC,AB,内错角相等,两直线平行;
②∵∠DAB+∠ABC=180°,
∴AD∥BC(同旁内角互补,两直线平行),
故答案为:AD,BC,同旁内角互补,两直线平行;
③∵DC∥AB,
∴∠3=∠A(两直线平行,同位角相等),
故答案为:DC,AB,两直线平行,同位角相等;
④∵DC∥AB,
∴∠C+∠ABC=180°,
故答案为:DC,AB,两直线平行,同旁内角互补.
点评 本题考查了平行线的判定和性质,熟练掌握平行线的判定和性质是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
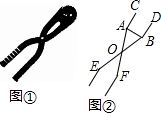 双十一期间,某店铺推出的如图①所示的雪球夹销售火爆,其形状可近似的看成图②所示的图形,当雪球夹闭合时,测得∠AOB=28°,OA=OB=14厘米,求这个雪球夹制作的雪球的直径AB的长度.(精确到1厘米)
双十一期间,某店铺推出的如图①所示的雪球夹销售火爆,其形状可近似的看成图②所示的图形,当雪球夹闭合时,测得∠AOB=28°,OA=OB=14厘米,求这个雪球夹制作的雪球的直径AB的长度.(精确到1厘米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
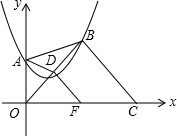 如图,抛物线y=a(x-1)2+$\sqrt{2}$(a≠0)经过y轴正半轴上的点A,点B,C分别是此抛物线和x轴上的动点,点D在OB上,且AD平分△ABO的面积,过D作DF∥BC交x轴于F点,则DF的最小值为$\frac{\sqrt{2}}{2}$.
如图,抛物线y=a(x-1)2+$\sqrt{2}$(a≠0)经过y轴正半轴上的点A,点B,C分别是此抛物线和x轴上的动点,点D在OB上,且AD平分△ABO的面积,过D作DF∥BC交x轴于F点,则DF的最小值为$\frac{\sqrt{2}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
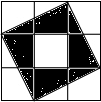 小明把如图所示的3×3的正方形网格纸板挂在墙上玩飞镖游戏(每次飞镖均落在纸板上,且落在纸板的任何一个点的机会都相等),则飞镖落在阴影区域(四个全等的直角三角形的每个顶点都在格点上)的概率是( )
小明把如图所示的3×3的正方形网格纸板挂在墙上玩飞镖游戏(每次飞镖均落在纸板上,且落在纸板的任何一个点的机会都相等),则飞镖落在阴影区域(四个全等的直角三角形的每个顶点都在格点上)的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{9}$ | D. | $\frac{5}{9}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com