
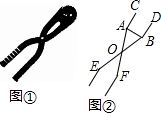
 双十一期间,某店铺推出的如图①所示的雪球夹销售火爆,其形状可近似的看成图②所示的图形,当雪球夹闭合时,测得∠AOB=28°,OA=OB=14厘米,求这个雪球夹制作的雪球的直径AB的长度.(精确到1厘米)
双十一期间,某店铺推出的如图①所示的雪球夹销售火爆,其形状可近似的看成图②所示的图形,当雪球夹闭合时,测得∠AOB=28°,OA=OB=14厘米,求这个雪球夹制作的雪球的直径AB的长度.(精确到1厘米)分析 如图②中,作OM⊥AB于M,在RT△AOM中,利用sin∠AOM=$\frac{AM}{AO}$求出AM,即可解决问题.
解答 解:如图②中,作OM⊥AB于M,则∠AMO=90°,
∵OA=OB,
∴AB=2AM,∠AOM=$\frac{1}{2}$∠AOB=$\frac{1}{2}$×28°=14°,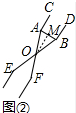
在RT△AOM中,∠AMO=90°,∠AOM=14°,OA=14,
∴sin∠AOM=$\frac{AM}{AO}$,
∴AM=O•sin∠AOM=14×sin14°≈14×0.24=3.36,
∴AB=2AM=6.72≈7(厘米).
答:这个雪球夹制作的雪球的直径AB的长度约为7厘米.
点评 本题考查解直角三角形的有关知识、等腰三角形的性质.解题的关键是转化为直角三角形去思考,体现了转化的思想,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
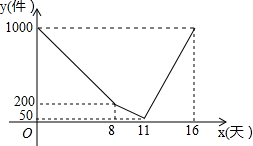 某厂家开发一种新产品,现有一定的库存量,投入市场试销,在试销期间不生产,试销结束后,厂家开始正式投入生产,当库存量不多时,厂家提高了工作效率.该产品每天的销售量相同时,库存量y(件)与销售天数(x)之间的函数关系如图所示)库存量=原有库存量+日生产量-日销售量)
某厂家开发一种新产品,现有一定的库存量,投入市场试销,在试销期间不生产,试销结束后,厂家开始正式投入生产,当库存量不多时,厂家提高了工作效率.该产品每天的销售量相同时,库存量y(件)与销售天数(x)之间的函数关系如图所示)库存量=原有库存量+日生产量-日销售量)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
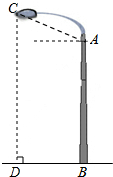 如图,某广场有一灯柱AB高7.5米,灯的顶端C离灯柱顶端A的距离CA为1.7米,且∠CAB=110°,求灯的顶端C距离地面的高度CD.(结果精确到0.1米)
如图,某广场有一灯柱AB高7.5米,灯的顶端C离灯柱顶端A的距离CA为1.7米,且∠CAB=110°,求灯的顶端C距离地面的高度CD.(结果精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
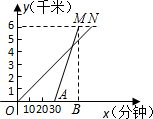 清明小长假期间,小明和小亮相约从学校出发,去距学校6千米的三国古城遗址公园游玩,小明步行但小亮骑自行车,在去公园的全过程中,骑自行车的小亮同学比步行的小明同学少用40分钟,已知骑自行车的速度是步行速度的3倍.
清明小长假期间,小明和小亮相约从学校出发,去距学校6千米的三国古城遗址公园游玩,小明步行但小亮骑自行车,在去公园的全过程中,骑自行车的小亮同学比步行的小明同学少用40分钟,已知骑自行车的速度是步行速度的3倍.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 推理填空:
推理填空:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com