
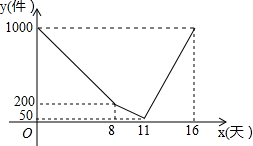
 某厂家开发一种新产品,现有一定的库存量,投入市场试销,在试销期间不生产,试销结束后,厂家开始正式投入生产,当库存量不多时,厂家提高了工作效率.该产品每天的销售量相同时,库存量y(件)与销售天数(x)之间的函数关系如图所示)库存量=原有库存量+日生产量-日销售量)
某厂家开发一种新产品,现有一定的库存量,投入市场试销,在试销期间不生产,试销结束后,厂家开始正式投入生产,当库存量不多时,厂家提高了工作效率.该产品每天的销售量相同时,库存量y(件)与销售天数(x)之间的函数关系如图所示)库存量=原有库存量+日生产量-日销售量)分析 (1)根据题意列算式即可得到结论;
(2)设y与x之间的函数关系式为:y=kx+b,应用待定系数法即可得到结论;
(3)根据题意列方程即可得到结论.
解答 解:(1)(1000-200)÷8=100(件);
答:当天销售新产品的件数为100件;
(2)设y与x之间的函数关系式为:y=kx+b,
将(8,200),(11,50)代入得:$\left\{\begin{array}{l}{8k+b=200}\\{11k+b=50}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-50}\\{b=600}\end{array}\right.$.
则y=-50x+600;
(3)设原来生产的产品件数为m件,
由题意得:200-100×(11-8)+(11-8)m=50,
解得:m=50,
设第11天后每天生产的产品件数为n件,
由题意得:50+(16-11)n-100(16-11)=1000,
解得:n=290,
则m-n=290-50=240.
答:11天后每天比原来多生产的产品件数为240件.
点评 本题考查了一次函数的应用,待定系数法求一次函数的解析式的运用,解答时分析理解函数的意义是关键.


科目:初中数学 来源: 题型:解答题
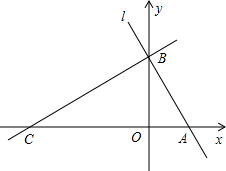 如图,平面直角坐标系中,直线l分别交x轴、y轴于A、B两点,点A的坐标为(1,0)∠ABO=30°,过点B的直线y=$\frac{{\sqrt{3}}}{3}$x+m与x轴交于点C.
如图,平面直角坐标系中,直线l分别交x轴、y轴于A、B两点,点A的坐标为(1,0)∠ABO=30°,过点B的直线y=$\frac{{\sqrt{3}}}{3}$x+m与x轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AB为⊙O的直径,四边形ABCD为⊙O的内接四边形,点P在BA的延长线上,PD与⊙O相切,D为切点,若∠BCD=120°,则∠APD的大小为( )
如图,AB为⊙O的直径,四边形ABCD为⊙O的内接四边形,点P在BA的延长线上,PD与⊙O相切,D为切点,若∠BCD=120°,则∠APD的大小为( )| A. | 45° | B. | 40° | C. | 35° | D. | 30° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
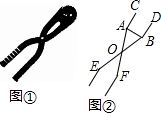 双十一期间,某店铺推出的如图①所示的雪球夹销售火爆,其形状可近似的看成图②所示的图形,当雪球夹闭合时,测得∠AOB=28°,OA=OB=14厘米,求这个雪球夹制作的雪球的直径AB的长度.(精确到1厘米)
双十一期间,某店铺推出的如图①所示的雪球夹销售火爆,其形状可近似的看成图②所示的图形,当雪球夹闭合时,测得∠AOB=28°,OA=OB=14厘米,求这个雪球夹制作的雪球的直径AB的长度.(精确到1厘米)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com