
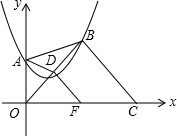
 如图,抛物线y=a(x-1)2+$\sqrt{2}$(a≠0)经过y轴正半轴上的点A,点B,C分别是此抛物线和x轴上的动点,点D在OB上,且AD平分△ABO的面积,过D作DF∥BC交x轴于F点,则DF的最小值为$\frac{\sqrt{2}}{2}$.
如图,抛物线y=a(x-1)2+$\sqrt{2}$(a≠0)经过y轴正半轴上的点A,点B,C分别是此抛物线和x轴上的动点,点D在OB上,且AD平分△ABO的面积,过D作DF∥BC交x轴于F点,则DF的最小值为$\frac{\sqrt{2}}{2}$. 分析 设点B的坐标为(m,a(m-1)2+$\sqrt{2}$),点C坐标为(n,0),由AD平分△ABO的面积可知点D为线段OB的中点,结合DF∥BC可知DF是△OBC的中位线,即DF=$\frac{1}{2}$BC,用两点间的距离公式表示出线段BC的长度,根据实数的平方非负可找出BC的最小值,从而得出结论.
解答 解:设点B的坐标为(m,a(m-1)2+$\sqrt{2}$),点C坐标为(n,0).
∵点D在OB上,且AD平分△ABO的面积,
∴OD=BD,
又∵DF∥BC,
∴DF是△OBC的中位线,
∴DF=$\frac{1}{2}$BC.
根据两点间的距离公式可知:
BC2=(m-n)2+$[a(m-1)^{2}+\sqrt{2}]^{2}$=(m-n)2+a2(m-1)4+2$\sqrt{2}$a(m-1)2+2,
结合抛物线开口向上可知a>0,
∴(m-n)2≥0,a2(m-1)4≥0,2$\sqrt{2}$a(m-1)2≥0,
∴BC2≥2,
∴BC=$\sqrt{2}$.
∵DF=$\frac{1}{2}$BC,
∴DF≥$\frac{\sqrt{2}}{2}$.
故答案为:$\frac{\sqrt{2}}{2}$.
点评 本题考查了二次函数的应用、两点间距离公式以及实数的平方非负,解题的关键是根据实数的平方非负找出线段BC的最小值.本题属于中档题,难度不大,巧妙的利用了两点间的距离公式寻找最值,两点间的距离公式虽说高中知识,单在初中阶段我们已经经常用到,此处使用给做题带来了极大的方便,故在日常做题中应适度的增加该部分的练习.


科目:初中数学 来源: 题型:填空题
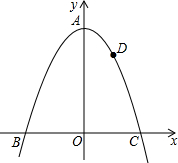 如图,过点D(1,3)的抛物线y=-x2+k的顶点为A,与x轴交于B、C两点,若点P是y轴上一点,则PC+PD的最小值为3$\sqrt{2}$.
如图,过点D(1,3)的抛物线y=-x2+k的顶点为A,与x轴交于B、C两点,若点P是y轴上一点,则PC+PD的最小值为3$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | “打开电视机,正在播百家讲坛”是必然事件 | |
| B. | “在标准大气压下,水加热到100℃会沸腾”是必然事件 | |
| C. | 一组数据2,3,4,5,5,6的众数和中位数都是5 | |
| D. | “篮球运动员在罚球线上投篮一次,未投中”是不可能事件 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 推理填空:
推理填空:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com