
分析 (1)根据已知分式的特点直接写出第6个即可;
(2)把已知等式两边除以3,变形后整体代入化简即可.
解答 解:(1)第6个分式为:$-\frac{12b}{(a-1)^{6}}$;
(2)由3a-4b=3可得:a-1=$\frac{4b}{3}$,
把a-1=$\frac{4b}{3}$,代入$\frac{6{b}^{2}}{(a-1)^{2}}$-$\frac{8{b}^{4}}{(a-1)^{4}}$=$\frac{6{b}^{2}}{(\frac{4b}{3})^{2}}$-$\frac{8{b}^{4}}{(\frac{4b}{3})^{4}}$=$\frac{27}{8}$-$\frac{81}{32}$=$\frac{27}{32}$.
点评 此题主要考查分式的规律探索和分式的化简,会根据题意进行适当变形整体代入是解题的关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
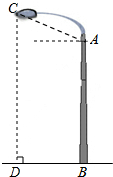 如图,某广场有一灯柱AB高7.5米,灯的顶端C离灯柱顶端A的距离CA为1.7米,且∠CAB=110°,求灯的顶端C距离地面的高度CD.(结果精确到0.1米)
如图,某广场有一灯柱AB高7.5米,灯的顶端C离灯柱顶端A的距离CA为1.7米,且∠CAB=110°,求灯的顶端C距离地面的高度CD.(结果精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
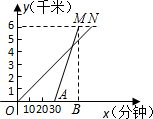 清明小长假期间,小明和小亮相约从学校出发,去距学校6千米的三国古城遗址公园游玩,小明步行但小亮骑自行车,在去公园的全过程中,骑自行车的小亮同学比步行的小明同学少用40分钟,已知骑自行车的速度是步行速度的3倍.
清明小长假期间,小明和小亮相约从学校出发,去距学校6千米的三国古城遗址公园游玩,小明步行但小亮骑自行车,在去公园的全过程中,骑自行车的小亮同学比步行的小明同学少用40分钟,已知骑自行车的速度是步行速度的3倍.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | “打开电视机,正在播百家讲坛”是必然事件 | |
| B. | “在标准大气压下,水加热到100℃会沸腾”是必然事件 | |
| C. | 一组数据2,3,4,5,5,6的众数和中位数都是5 | |
| D. | “篮球运动员在罚球线上投篮一次,未投中”是不可能事件 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 推理填空:
推理填空:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com