
如图,△OAB中,OA =" OB" = 10,∠AOB =
80°,以点O为圆心,6为半径的优弧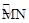 分别交OA,OB于点M,N.
分别交OA,OB于点M,N.
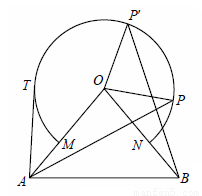
(1)点P在右半弧上(∠BOP是锐角),将OP绕点O逆时针旋转80°得OP′.
求证:AP = BP′;
(2)点T在左半弧上,若AT与弧相切,求点T到OA的距离;
(3)设点Q在优弧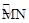 上,当△AOQ的面积最大时,直接写出∠BOQ的度数.
上,当△AOQ的面积最大时,直接写出∠BOQ的度数.
(1)根据已知得出∠AOP=∠BOP′,从进而由SAS得出△AOP≌△BOP′,即可得出答案。
(2)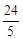
(3)10°或170°
【解析】
分析:(1)根据已知得出∠AOP=∠BOP′,从进而由SAS得出△AOP≌△BOP′,即可得出答案。
(1)证明:如图1,∵∠AOP=∠AOB+∠BOP=80°+∠BOP,
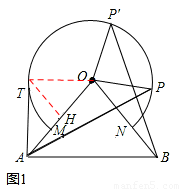
∠BOP′=∠POP′+∠BOP=80°+∠BOP,
∴∠AOP=∠BOP′。
∵在△AOP和△BOP′中,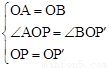 ,
,
∴△AOP≌△BOP′(SAS)。
∴AP=BP′。
(2)利用切线的性质得出∠ATO=90°,再利用勾股定理求出AT的长,进而得出TH的长即可得出答案。
解:如图1,连接OT,过点T作TH⊥OA于点H,
∵AT与 相切,∴∠ATO=90°。
相切,∴∠ATO=90°。
∴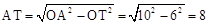 。
。
∵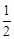 ×OA×TH=
×OA×TH=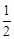 ×AT×OT,
×AT×OT,
∴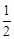 ×10×TH=
×10×TH=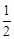 ×8×6,解得:TH=
×8×6,解得:TH=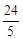 。
。
∴点T到OA的距离为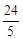 。
。
(3)如图2,当OQ⊥OA时,△AOQ的面积最大。理由如下:
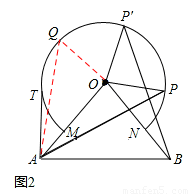
当Q点在优弧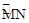 左侧上,
左侧上,
∵OQ⊥OA,
∴QO是△AOQ中最长的高,则△AOQ的面积最大。
∴∠BOQ=∠AOQ+∠AOB=90°+80°=170°。
当Q点在优弧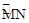 右侧上,
右侧上,
∵OQ⊥OA,
∴QO是△AOQ中最长的高,则△AOQ的面积最大。
∴∠BOQ=∠AOQ--∠AOB=90°-80°=10°。
综上所述:当∠BOQ的度数为10°或170°时,△AOQ的面积最大。


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
| 2 |
 向以每秒2个单位匀速运动,当点P到达点O时,两点同时停止运动,设运动的时间为t秒.
向以每秒2个单位匀速运动,当点P到达点O时,两点同时停止运动,设运动的时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•河北)如图,△OAB中,OA=OB=10,∠AOB=80°,以点O为圆心,6为半径的优弧
(2013•河北)如图,△OAB中,OA=OB=10,∠AOB=80°,以点O为圆心,6为半径的优弧 |
| MN |
 |
| MN |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com