
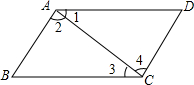
 如图,下列判断错误的是( )
如图,下列判断错误的是( )| A. | 如果∠2=∠4,那么AB∥CD | B. | 如果∠1=∠3,那么AB∥CD | ||
| C. | 如果∠BAD+∠D=180,那么AB∥CD | D. | 如果∠BAD+∠B=180,那么AD∥CD |
分析 根据平行线的判定定理即可求解.
解答 解:A、由内错角相等,两直线平行可知,如果∠2=∠4,那么AB∥CD是正确的,不符合题意;
B、由内错角相等,两直线平行可知,如果∠1=∠3,那么AD∥BC,原来的说法是错误的,符合题意;
C、由同旁内角互补,两直线平行可知,如果∠BAD+∠D=180,那么AB∥CD是正确的,不符合题意;
D、由同旁内角互补,两直线平行可知,如果∠BAD+∠B=180,那么AD∥CD是正确的,不符合题意.
故选B.
点评 考查了平行线的判定,关键是熟练掌握(1)定理1:两条直线被第三条所截,如果同位角相等,那么这两条直线平行. 简单说成:同位角相等,两直线平行.(2)定理2:两条直线被第三条所截,如果内错角相等,那么这两条直线平行.简单说成:内错角相等,两直线平行.(3)定理3:两条直线被第三条所截,如果同旁内角互补,那么这两条直线平行.简单说成:同旁内角互补,两直线平行.(4)定理4:两条直线都和第三条直线平行,那么这两条直线平行.(5)定理5:在同一平面内,如果两条直线同时垂直于同一条直线,那么这两条直线平行.


科目:初中数学 来源: 题型:解答题
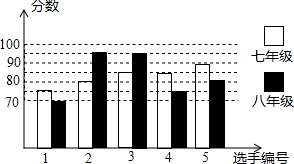 我县某初中举行“中学生与社会”作文大赛,七年级、八年级根据初赛成绩,各选出5名选手组成七年级代表队和八年级代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.
我县某初中举行“中学生与社会”作文大赛,七年级、八年级根据初赛成绩,各选出5名选手组成七年级代表队和八年级代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.| 平均数 (分) | 中位数 (分) | 众数 (分) | |
| 七年级 | 83 | 85 | 85 |
| 八年级 | 83 | 80 | 95 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com