
分析 (1)先求得x+2<0,然后利用$\sqrt{{a}^{2}}=|a|$绝对值进行化简即可;
(2)先将分式的分子分母进行分解,然后再约分、计算即可.
解答 解:(1)∵x<-2,
∴x+2<0.
∴$\sqrt{(x+2)^{2}}$=|x+2|=-x-2;
(2)原式=$\frac{2(x+y)}{5{a}^{2}b}•\frac{10a{b}^{2}}{(x+y)(x-y)}$=$\frac{4b}{a(x-y)}$.
故答案为:-x-2;$\frac{4b}{a(x-y)}$.
点评 本题主要考查的是二次根式的性质和分式的化简,掌握二次根式的性质和分式化简的方法和步骤是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
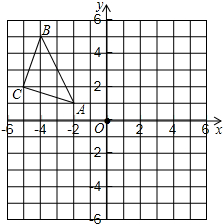 如图,△ABC在平面直角坐标系中,其中,点A、B、C的坐标分别为A(-2,1),B(-4,5),C(-5,2).
如图,△ABC在平面直角坐标系中,其中,点A、B、C的坐标分别为A(-2,1),B(-4,5),C(-5,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
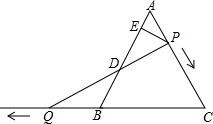 如图,已知△ABC是等腰三角形,且∠C=60°,AB=10,点P是AC边上一动点,由点A向点C运动(点P与点A、C不重合),Q是CB延长线上一点,与 点P同时以相同的速度由点B向CB延长线方向运动(点Q与点B不重合),过点P作PE⊥AB于点E,连结PQ交AB于点D.
如图,已知△ABC是等腰三角形,且∠C=60°,AB=10,点P是AC边上一动点,由点A向点C运动(点P与点A、C不重合),Q是CB延长线上一点,与 点P同时以相同的速度由点B向CB延长线方向运动(点Q与点B不重合),过点P作PE⊥AB于点E,连结PQ交AB于点D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 总体 | B. | 个体 | C. | 总体的一个样本 | D. | 普查方式 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2017届湖北省赤壁市九年级下学期第一次模拟(调研)考试数学试卷(解析版) 题型:填空题
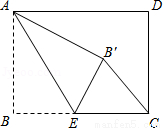
如图,矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处.当△CEB′为直角三角形时,BE的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com