
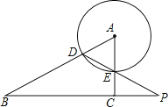
如图,在Rt△ABC中,∠ACB=90°,半径为1的圆A与边AB相交于点D,与边AC相交于点E,连接DE并延长,与线段BC的延长线交于点P.已知tan∠BPD= ,CE=2,则△ABC的周长是
,CE=2,则△ABC的周长是
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:初中数学 来源:2018年广东省东莞市堂镇六校考数学模拟试卷 题型:填空题
已知A(a﹣5,2b﹣1)在y轴上,B(3a+2,b+3)在x轴上,则C(a,b)向左平移2个单位长度再向上平移3个单位长度后的坐标为_____.
查看答案和解析>>
科目:初中数学 来源:江苏省镇江市润州区2018届九年级中考模拟试卷数学试卷 题型:解答题
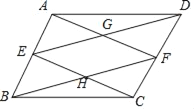
如图,在平行四边形ABCD中,E,F分别是AB,CD的中点,AF与DE相交于点G,BF与CE相交于点H.
(1)求证:四边形EHFG是平行四边形;
(2)①若四边形EHFG是菱形,则平行四边形ABCD必须满足条件 ;
②若四边形EHFG是矩形,则平行四边形ABCD必须满足条件 .
查看答案和解析>>
科目:初中数学 来源:江苏省镇江市润州区2018届九年级中考模拟试卷数学试卷 题型:单选题
下列说法正确的是( )
A. 了解“孝感市初中生每天课外阅读书籍时间的情况”最适合的调查方式是全面调查
B. 甲乙两人跳绳各10次,其成绩的平均数相等,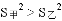 ,则甲的成绩比乙稳定
,则甲的成绩比乙稳定
C. 三张分别画有菱形,等边三角形,圆的卡片,从中随机抽取一张,恰好抽到中心对称图形卡片的概率是
D. “任意画一个三角形,其内角和是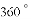 ”这一事件是不可能事件
”这一事件是不可能事件
查看答案和解析>>
科目:初中数学 来源:浙江省宁波市南三县2018届九年级中考模拟数学试卷(4) 题型:解答题
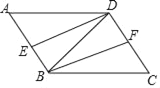
已知:如图,在?ABCD中,DE平分∠ADB,交AB于E,BF平分∠CBD,交CD于F.
(1)求证:△ADE≌△CBF;
(2)当AD与BD满足什么关系时,四边形DEBF是矩形?请说明理由.
查看答案和解析>>
科目:初中数学 来源:浙江省宁波市南三县2018届九年级中考模拟数学试卷(4) 题型:单选题
下列命题中,真命题的个数有( )
①如果两条直线都与第三条直线平行,那么这两条直线也互相平行.
②过直线外一点有且只有一条直线与这条直线平行.
③两条直线被第三条直线所截,同旁内角互补.
④内错角相等,两直线平行.
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源:2018年湖南省长沙市中考数学模拟试卷(3月份) 题型:解答题
设a,b是任意两个不等实数,我们规定:满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b].对于一个函数,如果它的自变量x与函数值y满足:当m≤x≤n时,有m≤y≤n,我们就称此函数是闭区间[m,n]上的“闭函数”.如函数y=﹣x+4,当x=1时,y=3;当x=3时,y=1,即当1≤x≤3时,恒有1≤y≤3,所以说函数y=﹣x+4是闭区间[1,3]上的“闭函数”,同理函数y=x也是闭区间[1,3]上的“闭函数”.
(1)反比例函数y= 是闭区间[1,2018]上的“闭函数”吗?请判断并说明理由;
是闭区间[1,2018]上的“闭函数”吗?请判断并说明理由;
(2)如果已知二次函数y=x2﹣4x+k是闭区间[2,t]上的“闭函数”,求k和t的值;
(3)如果(2)所述的二次函数的图象交y轴于C点,A为此二次函数图象的顶点,B为直线x=1上的一点,当△ABC为直角三角形时,写出点B的坐标.
查看答案和解析>>
科目:初中数学 来源:2018年湖南省长沙市中考数学模拟试卷(3月份) 题型:单选题
下列计算正确的是( )
A. a3+a2=a5 B. 3a﹣2=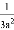 C. a6b÷a2=a3b D. (﹣ab3)2=a2b6
C. a6b÷a2=a3b D. (﹣ab3)2=a2b6
查看答案和解析>>
科目:初中数学 来源:山东省青岛市2018年中考数学模拟试卷(6月份) 题型:解答题
数学问题:计算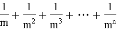 (其中m,n都是正整数,且m≥2,n≥1).
(其中m,n都是正整数,且m≥2,n≥1).
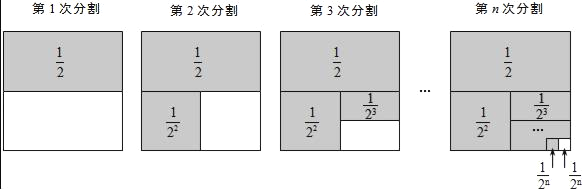
探究问题:为解决上面的数学问题,我们运用数形结合的思想方法,通过不断地分割一个面积为1的正方形,把数量关系和几何图形巧妙地结合起来,并采取一般问题特殊化的策略来进行探究.
探究一:计算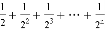 .
.
第1次分割,把正方形的面积二等分,其中阴影部分的面积为 ;
;
第2次分割,把上次分割图中空白部分的面积继续二等分,阴影部分的面积之和为 +
+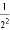 ;
;
第3次分割,把上次分割图中空白部分的面积继续二等分,…;
…
第n次分割,把上次分割图中空白部分的面积最后二等分,所有阴影部分的面积之和为 +
+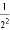 +
+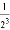 +…+
+…+ ,最后空白部分的面积是
,最后空白部分的面积是 .
.
根据第n次分割图可得等式: +
+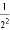 +
+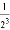 +…+
+…+ =1﹣
=1﹣ .
.
探究二:计算 +
+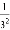 +
+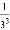 +…+
+…+ .
.
第1次分割,把正方形的面积三等分,其中阴影部分的面积为 ;
;
第2次分割,把上次分割图中空白部分的面积继续三等分,阴影部分的面积之和为 +
+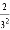 ;
;
第3次分割,把上次分割图中空白部分的面积继续三等分,…;
…
第n次分割,把上次分割图中空白部分的面积最后三等分,所有阴影部分的面积之和为 +
+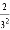 +
+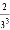 +…+
+…+ ,最后空白部分的面积是
,最后空白部分的面积是 .
.
根据第n次分割图可得等式: +
+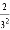 +
+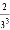 +…+
+…+ =1﹣
=1﹣ ,
,
两边同除以2,得 +
+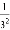 +
+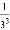 +…+
+…+ =
= ﹣
﹣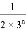 .
.
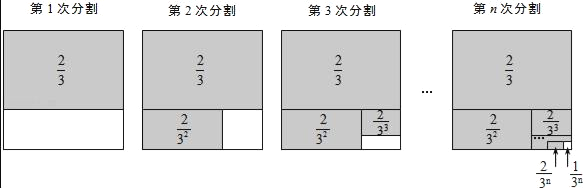
探究三:计算 +
+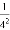 +
+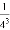 +…+
+…+ .
.
(仿照上述方法,只画出第n次分割图,在图上标注阴影部分面积,并写出探究过程)

解决问题:计算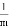 +
+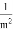 +
+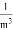 +…+
+…+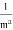 .
.
(只需画出第n次分割图,在图上标注阴影部分面积,并完成以下填空)
根据第n次分割图可得等式:_________,
所以,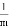 +
+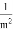 +
+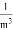 +…+
+…+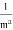 =________.
=________.
拓广应用:计算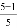 +
+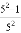 +
+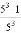 +…+
+…+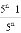 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com