
����Ŀ��Ϊ�˽��п�������Ŀѵ�������ijУ�Ӿ��꼶ѧ���������ȡ����ѧ��������һ���п�������Ŀ���ԣ��Ѳ��Խ����ΪA��B��C��D�ĸ��ȼ������������Խ�����Ƴ�����ͼ��ʾ������������ͳ��ͼ������ͳ��ͼ���ṩ����Ϣ�����۴�����ǣ� �� 
A.���γ������Ե�ѧ��������40
B.��ͼ1�У��Ϧ��Ķ�����126��
C.��У���꼶��ѧ��500��������D��������Ϊ80
D.�ӱ���ѧ���������ȡһλ������λѧ���ijɼ���A���ĸ���Ϊ0.2
���𰸡�C
���������⣺A�����γ������Ե�ѧ�������ǣ�12��30%=40���ˣ�����ȷ���������⣻ B���� ![]() ��360��=126�㣬�Ϧ��Ķ�����126�㣬�ʴ�ѡ����ȷ���������⣻
��360��=126�㣬�Ϧ��Ķ�����126�㣬�ʴ�ѡ����ȷ���������⣻
C����У���꼶��ѧ��500��������D��������Ϊ��500�� ![]() =100���ˣ����ʴ�ѡ����������⣻
=100���ˣ����ʴ�ѡ����������⣻
D���ӱ���ѧ���������ȡһλ������λѧ���ijɼ���A���ĸ���Ϊ�� ![]() =0.2����ȷ���������⣻
=0.2����ȷ���������⣻
��ѡ��C��
�����㾫������������ͳ��ͼ������ͳ��ͼ����Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪������ر�ʾ������������������ռ�İٷֱȣ����Dz�������ر�ʾ��ÿ����Ŀ�ľ�����Ŀ�Լ�����ı仯�����������ر�ʾ��ÿ����Ŀ�ľ�����Ŀ�����Dz�������ر�ʾ��������������������ռ�İٷֱ��Լ�����ı仯�����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧУ���ڸ�������ͼ����Էḻͬѧ�ǵĿ����Ļ����Ϊ�˸������Ĵ�������鼮��ѧУ��ί�ԡ�����ϲ�����鼮��Ϊ���⣬��ѧ����ϲ����һ���鼮���ͽ�������������飬�ռ��������ݺ��Ƴ���������δ��ɵ�ͳ��ͼ�������ͼ1��ͼ2�ṩ����Ϣ������������⣺ 
��1������γ��������У�һ�������˶�����ѧ����
��2���������ͳ��ͼ��ͼ1������������
��3���������ͳ��ͼ��ͼ2���У�������������Ӧ��Բ�ĽǵĶ�����
��4�����������ѧ����ѧ��1800������ô���������ϲ���������鼮��ѧ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��PBΪ��O�����ߣ�BΪ�е㣬ֱ��PO�����ڵ�E��F������B��PO�Ĵ���BA������Ϊ��D������O�ڵ�A���ӳ�AO���O���ڵ�C������BC��AF��
��1����֤��ֱ��PAΪ��O�����ߣ�
��2����̽���߶�EF��OD��OP֮��ĵ�����ϵ��������֤����
��3����BC=6��tan��F= ![]() ����cos��ACB��ֵ���߶�PE�ij���
����cos��ACB��ֵ���߶�PE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���κ���ͼ��Ķ�������ΪC��1��0����ֱ��y=x+m��ö��κ�����ͼ����A��B���㣬����A�������Ϊ��3��4����B����y���ϣ�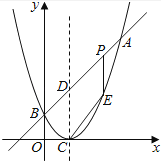
��1����m��ֵ��������κ����Ĺ�ϵʽ��
��2��PΪ�߶�AB�ϵ�һ�����㣨��P��A��B���غϣ�����P��x��Ĵ�����������κ�����ͼ���ڵ�E�����߶�PE�ij�Ϊh����P�ĺ�����Ϊx����h��x֮��ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
��3��DΪֱ��AB��������κ���ͼ��Գ���Ľ��㣬���߶�AB���Ƿ����һ��P��ʹ���ı���DCEP��ƽ���ı��Σ������ڣ��������ʱP������ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ���ѧ���������ʣ�������չ��������̨��ƹ��������������������Ҫ��ѧ�����벢��ֻ��ѡ��һ�Ϊ�˽�ѡ������������Ŀ��ѧ�������������ȡ�˲���ѧ�����е��飬�����Ƴ�����������������ͳ��ͼ�������ͳ��ͼ�ش��������⣮��Ҫ��д����Ҫ�Ľ����̣� 
��1����λһ�������˶�����ѧ����
��2����ȫ����ͳ��ͼ��
��3������ѧУ��������1300�ˣ������ѡ��������Ŀ��ѧ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���C=90�㣬AB=10cm��BC=8cm����P�ӵ�A��AC���C��1cm/s���ٶ��˶���ͬʱ��Q�ӵ�C��CB���B��2cm/s���ٶ��˶�����Q�˶�����Bֹͣ�������˶������У��ı���PABQ�������СֵΪ�� �� 
A.19cm2
B.16cm2
C.15cm2
D.12cm2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м��������ǣ� ��
A.![]() =4
=4
B.32��3��1=3
C.20��2��2= ![]()
D.����3��102��3=��2.7��107
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����衰�Ҹ������������조��ɫ��չ������С�����������ˮ������һ��������Ƕ��������γɡ�ˮ�塢���������̡�����������̬�����¸�֣�����ѧ����ʵ����У�С���ں����������г��̵�����AC�ϵ�A��B����ֱ���ϰ�����������D���в������ֱ��á�DAC=30�㣬��DBC=60�㣬AB=200�ף�����������D����ˮ�ӱ���AC�ľ���ԼΪ�����ף���ȷ��1�ף� ![]() ��1.732����
��1.732���� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ķ����в��ϣ�
���⣺��ͼ1���ڵȱ�������ABC����һ��P����PA=2��PB= ![]() ��PC=1�����BPC�����Ĵ�С�͵ȱ�������ABC�ı߳���
��PC=1�����BPC�����Ĵ�С�͵ȱ�������ABC�ı߳���
����ͬѧ��˼·�ǣ�����BPC�Ƶ�B��ʱ����ת60�㣬������ת���ͼ�Σ���ͼ2��������PP�䣬�ɵá�P��PC�ǵȱ������Σ�����PP��A����ֱ�������Σ��ɹ��ɶ������涨����֤�������ԡ�AP��B=150�㣬����BPC=��AP��B=150�㣬��������ȱߡ�ABC�ı߳�Ϊ ![]() ������õ������
������õ������
����ο�����ͬѧ��˼·��̽��������������⣺��ͼ3����������ABCD����һ��P����PA= ![]() ��BP=
��BP= ![]() ��PC=1�����BPC�����Ĵ�С��������ABCD�ı߳���
��PC=1�����BPC�����Ĵ�С��������ABCD�ı߳���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com