
已知抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴.
(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,当△PAC的周长最小时,求点P的坐标,并求出此时的周长;
(3)在直线l上是否存在点M,使△MAC为直角三角形?若存在,请写出所有符合条件的点M的坐标;若不存在,请说明理由.
(1)y=-x2+2x+3;(2)P(1,2), ;(3).M(1,
;(3).M(1, )(1,-
)(1,- )(1,1)(1,0).
)(1,1)(1,0).
解析试题分析:(1)直接将A、B、C三点坐标代入抛物线的解析式中求出待定系数即可.
(2)由图知:A、B点关于抛物线的对称轴对称,那么根据抛物线的对称性以及两点之间线段最短可知:若连接BC,那么BC与直线l的交点即为符合条件的P点.
(3)由于△MAC的腰和底没有明确,因此要分三种情况来讨论:①MA=AC、②MA=MC、②AC=MC;可先设出M点的坐标,然后用M点纵坐标表示△MAC的三边长,再按上面的三种情况列式求解.
试题解析:(1)将A(-1,0)、B(3,0)、C(0,3)代入抛物线y=ax2+bx+c中,得: ,解得:
,解得: 
∴抛物线的解析式:y=-x2+2x+3.
(2)y=-x2+2x+3的对称轴x=1,设点P为(1,p)
因为对称轴垂直平分AB,所以:PA=PB.
△PAC的周长=AC+PC+PA=AC+PC+PB
其中
当点B、P和C三点共线时,PC+PB存在最小值:
直线BC:y=-x+3,点P在直线BC上:p=-1+3=2
所以点P为(1,2),此时△PAC的周长最小值为
(3)抛物线的解析式为:x=- =1,设M(1,m),已知A(-1,0)、C(0,3),则:
=1,设M(1,m),已知A(-1,0)、C(0,3),则:
MA2=m2+4,MC2=m2-6m+10,AC2=10;
①若MA=MC,则MA2=MC2,得:
m2+4=m2-6m+10,得:m=1;
②若MA=AC,则MA2=AC2,得:
m2+4=10,得:m=± ;
;
③若MC=AC,则MC2=AC2,得:
m2-6m+10=10,得:m=0,m=6;
当m=6时,M、A、C三点共线,构不成三角形,不合题意,故舍去;
综上可知,符合条件的M点,且坐标为 M(1, )(1,-
)(1,- )(1,1)(1,0).
)(1,1)(1,0).
考点: 二次函数综合题.


科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系xOy中,边长为2的正方形OABC的顶点A、C分别在x轴、y轴的正半轴上,二次函数y=- x2+bx+c的图象经过B、C两点.
x2+bx+c的图象经过B、C两点.
(1)求b,c的值.
(2)结合函数的图象探索:当y>0时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知:抛物线 与x轴交于点A、B(A左B右),其中点B的坐标为(7,0),设抛物线的顶点为C.
与x轴交于点A、B(A左B右),其中点B的坐标为(7,0),设抛物线的顶点为C.
(1)求抛物线的解析式和点C的坐标;
(2)如图1,若AC交y轴于点D,过D点作DE∥AB交BC于E.点P为DE上一动点,PF⊥AC于F,PG⊥BC于G.设点P的横坐标为a,四边形CFPG的面积为y,求y与a的函数关系式和y的最大值;
(3)如图2,在条件(2)下,过P作PH⊥x轴于点H,连结FH、GH,是否存在点P,使得△PFH与△PHG相似?若存在,求出P点坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某汽车租赁公司拥有20辆汽车.据统计,当每辆车的日租金为400元时,可全部租出;当未租出的车将增加1辆,每辆车的日租金每增加50元,;公司平均每日的各项支出共4800元.设公司每日租出工辆车时,日收益为y元.(日收益=日租金收入一平均每日各项支出)
(1)公司每日租出x辆车时,每辆车的日租金为 元(用含x的代数式表示);
(2)当每日租出多少辆时,租赁公司日收益最大?最大是多少元?
(3)当每日租出多少辆时,租赁公司的日收益不盈也不亏?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,直线 与x轴、y轴分别交于点A、C,经过A、C两点的抛物线
与x轴、y轴分别交于点A、C,经过A、C两点的抛物线 与x轴的负半轴上另一交点为B,且tan∠CBO=3.
与x轴的负半轴上另一交点为B,且tan∠CBO=3.
(1)求该抛物线的解析式及抛物线的顶点D的坐标;
(2)若点P是射线BD上一点,且以点P、A、B为顶点的三角形与△ABC相似,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
小明投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数: ,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.
,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.
(1)设小明每月获得利润为w(元),求每月获得利润w(元)与销售单价x(元)之间的函数关系式,并确定自变量x的取值范围.
(2)当销售单价定为多少元时,每月可获得最大利润?每月的最大利润是多少?
(3)如果小明想要每月获得的利润不低于2000元,那么小明每月的成本最少需要多少元?
(成本=进价×销售量)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,抛物线y=ax2+bx+c经过点A(﹣3,0),B(0,3),C(1,0).
(1)求此抛物线的解析式.
(2)点P是直线AB上方的抛物线上一动点,(不与点A、B重合),过点P作x轴的垂线,垂足为F,交直线AB于点E,作PD⊥AB于点D.
①动点P在什么位置时,△PDE的周长最大,求出此时P点的坐标;
②连接PA,以AP为边作图示一侧的正方形APMN,随着点P的运动,正方形的大小、位置也随之改变.
当顶点M或N恰好落在抛物线对称轴上时,求出对应的P点的坐标.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某商品的进价为每件40元,售价为每件50元,每个月可卖出210件;如果每件商品的售价每上涨1元,则每个月少卖10件(每件售价不能高于65元).
设每件商品的售价上涨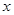 元(
元(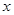 为正整数),每个月的销售利润为
为正整数),每个月的销售利润为 元.
元.
(1)求 与
与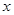 的函数关系式并直接写出自变量
的函数关系式并直接写出自变量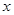 的取值范围;
的取值范围;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
(3)每件商品的售价定为多少元时,每个月的利润恰为2200元?根据以上结论,请你直接写出售价在什么范围时,每个月的利润不低于2200元?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,足球场上守门员在O处开出一高球,球从离地面1米的A处飞出(A在y轴上),运动员乙在距O点6米的B处发现球在自己头的正上方达到最高点M,距地面约4米高,球落地后又一次弹起.据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
(1)求足球开始飞出到第一次落地时,该抛物线的表达式.
(2)足球第一次落地点C距守门员多少米?(取 )
)
(3)运动员乙要抢到第二个落点D,他应再向前跑多少米?(取 )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com