
 一块边缘呈抛物线型的铁片如图放置,测得AB=20cm,抛物线顶点到AB边的距离为25cm,现要沿AB边向上依次截取宽度为4cm的矩形铁皮,建立如图所示的直角坐标系.
一块边缘呈抛物线型的铁片如图放置,测得AB=20cm,抛物线顶点到AB边的距离为25cm,现要沿AB边向上依次截取宽度为4cm的矩形铁皮,建立如图所示的直角坐标系.分析 (1)根据抛物线的顶点坐标为(0,25),可设其顶点式,将A点或B点坐标代入即可得;
(2)根据抛物线解析式求出第4块矩形铁皮的长,可得长、宽之比;
(3)若截得的铁皮是正方形,则铁皮的长2|x|=4,将x=2或x=-2代入解析式求出矩形总的高度y,判断是否为4的整数倍即可.
解答 解:(1)根据题意知,A(-10,0),顶点坐标为(0,25),
可设抛物线解析式为:y=ax2+25,
将A(-10,0)代入,得:100a+25=0,解得:a=-$\frac{1}{4}$,
故抛物线解析式为:y=-$\frac{1}{4}$x2+25;
(2)当y=4×4=16时,有-$\frac{1}{4}$x2+25=16,解得:x=±6,
则第四块矩形铁皮的长为2×6=12cm,
故第四块矩形铁皮的长与宽的比为12:4=3;
(3)若截得的铁皮是正方形,则铁皮的长2|x|=4,即x=±2,
当x=2时,y=-$\frac{1}{4}$×22+25=24=4×6,
故截得的第6个铁皮是正方形.
点评 本题主要考查二次函数的应用能力,求出抛物线解析式是基础,根据题意将矩形的长、宽转化成函数中的x与y并作出清晰判断是关键.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:解答题
 加图,四边形ABCD是王老六家的一块平行四边形田地,P为水井,现要把这块田地平均分给他的两个儿子,为了方便用水,要求两个儿子分到的地都与水井相邻,请你来设计一下,并说明你的理由.
加图,四边形ABCD是王老六家的一块平行四边形田地,P为水井,现要把这块田地平均分给他的两个儿子,为了方便用水,要求两个儿子分到的地都与水井相邻,请你来设计一下,并说明你的理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,四边形ABCD中,∠A=∠B=90°,E是AB的中点,DE平分∠ADC.
如图,四边形ABCD中,∠A=∠B=90°,E是AB的中点,DE平分∠ADC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
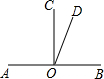 如图,直线AB过点O,OC、OD是直线AB同旁的两条射线,若∠BOD比∠COD的3倍还大20°,∠AOD比∠BOD的2倍小15°.求∠COD的度数.
如图,直线AB过点O,OC、OD是直线AB同旁的两条射线,若∠BOD比∠COD的3倍还大20°,∠AOD比∠BOD的2倍小15°.求∠COD的度数.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -36 | B. | 45 | C. | -55 | D. | 66 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边和相同的刻度分别为M,N、N重合,过角尺顶点C的射线OC就是∠AOB的平分线.请将上述应用问题改成几何问题.根据题意写出已知,求证,并完成证明过程.
如图,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边和相同的刻度分别为M,N、N重合,过角尺顶点C的射线OC就是∠AOB的平分线.请将上述应用问题改成几何问题.根据题意写出已知,求证,并完成证明过程.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com