
【题目】(1)若x,y都是实数,且y=![]() +
+![]() +8,求5x+13y+6的值;
+8,求5x+13y+6的值;
(2)已知△ABC的三边长分别为a,b,c,且满足![]() +b2-6b+9=0,求c的取值范围。
+b2-6b+9=0,求c的取值范围。
【答案】(1)125;(2)2<c<4.
【解析】
(1)根据二次根式有意义的条件可得出x的值,继而得出y的值,即可求出5x+13y+6的值后;
(2)已知等式左边后三项利用完全平方公式变形,根据非负数之和为0,非负数分别为0求出a与b的值,即可得出第三边c的范围.
(1)(1)∵要使y=![]() +
+![]() +8中的二次根式有意义
+8中的二次根式有意义
∴x-3≥0且3-x≤0,
∴x≥3且x≤3,
∴x=3,
∴y=![]() +
+![]() +8=0+0+8=8,
+8=0+0+8=8,
∴5x+13y+6=15+104+6=125
(2)∵![]() +b2-6b+9=0,
+b2-6b+9=0,
∴![]() +(b-3)2=0,
+(b-3)2=0,
又∵![]() ≥0,(b-3)2≥0,
≥0,(b-3)2≥0,
∴a-1=0,b-3=0,
∴a=1,b=3,
∴b-a<c<b+a
∴2<c<4.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=90°,点D是BC上一点,将△ABD沿AD翻折后得到△AED,边AE交BC于点F.


(1)如图①,当AE⊥BC时,写出图中所有与∠B相等的角: ;所有与∠C相等的角: .
(2)若∠C-∠B=50°,∠BAD=x°(0<x≤45) .
① 求∠B的度数;
②是否存在这样的x的值,使得△DEF中有两个角相等.若存在,并求x的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知E、F是□ABCD对角线AC上的两点,且BE⊥AC,DF⊥AC.

(1)请写出图中全等三角形(不再添加辅助线).
(2)求证:△ABE≌△CDF;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:已知方程a2![]() 2a
2a![]() 1=0,1
1=0,1![]() 2b
2b![]() b2=0且ab≠1,求
b2=0且ab≠1,求![]() 的值.
的值.
解:由a2![]() 2a
2a![]() 1=0及1
1=0及1![]() 2b
2b![]() b2=0,
b2=0,
可知a≠0,b≠0,
又∵ab≠1,![]() .
.
1![]() 2b
2b![]() b2=0可变形为
b2=0可变形为
![]() ,
,
根据a2![]() 2a
2a![]() 1=0和
1=0和![]() 的特征.
的特征.
![]() 、
、![]() 是方程x2
是方程x2![]() 2x
2x![]() 1=0的两个不相等的实数根,
1=0的两个不相等的实数根,
则![]() ,即
,即![]() .
.
根据阅读材料所提供的方法,完成下面的解答.
已知:3m2![]() 7m
7m![]() 2=0,2n2+7n
2=0,2n2+7n![]() 3=0且mn≠1,求
3=0且mn≠1,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BE和CE分别为△ABC的内角平分线和外角平分线,BE⊥AC于点H,CF平分∠ACB交BE于点F连接AE.则下列结论:①∠ECF=90°;②AE=CE;③![]() ;④∠BAC=2∠BEC;⑤∠AEH=∠BCF,正确的个数为( )
;④∠BAC=2∠BEC;⑤∠AEH=∠BCF,正确的个数为( )

A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中,每个小正方形的边长是1个单位长度)
(1)作出△ABC绕点A顺时针方向旋转90°后得到的△A1B1C1,并写出C1点的坐标 ;
(2)作出△ABC关于原点O成中心对称的△A2B2C2,并求出△ABC的面积 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角板中的两块直角三角尺的直角顶点C按如图所示的方式叠放在一起(其中,![]() ,
,![]() ;
;![]() ).
).

(1)①若![]() ,则
,则![]() 的度数为_____________;
的度数为_____________;
②若![]() ,则
,则![]() 的度数为_____________.
的度数为_____________.
(2)由(1)猜想![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
(3)当![]() 且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请写出
且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请写出![]() 角度所有可能的值(不必说明理由);若不存在,请说明理由.
角度所有可能的值(不必说明理由);若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
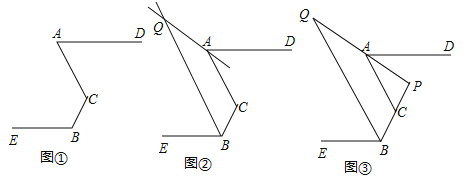
【题目】如图,已知:点![]() 不在同一条直线,
不在同一条直线,![]() .
.
(1)求证:![]() .
.
(2)如图②,![]() 分别为
分别为![]() 的平分线所在直线,试探究
的平分线所在直线,试探究![]() 与
与![]() 的数量关系;
的数量关系;
(3)如图③,在(2)的前提下,且有![]() ,直线
,直线![]() 交于点
交于点![]() ,
,![]() ,请直接写出
,请直接写出![]() ______________.
______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com