
����Ŀ������һ����ͯ��ǰϦ��ޭ���ؽ������������ض�ͯ����һ��ѧϰ��Ʒ���ȶ��Ȫ���ȪСѧ�����ض�ͯ�������г���ͳ�ƣ����ָ������ض�ͯ�����ֱ�Ϊ6����7����8����10����12�����������Σ�����ͳ�ƽ�����Ƴ�����ͼ��ʾ��������������ͳ��ͼ��
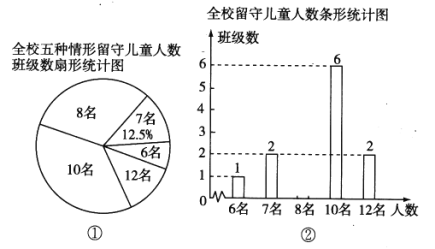
���������ͳ��ͼ������������⣺
(1)��У�ж��ٸ��༶������ȫ����ͳ��ͼ��
(2)��Уƽ��ÿ���ж��������ض�ͯ�����ض�ͯ�����������Ƕ��٣�
(3)����������Сѧ����60����ѧ�࣬������������ݣ����Ƹ���Сѧ���У����ж��������ض�ͯ��
���𰸡���1����У��16���༶����2����Уƽ��ÿ����9�����ض�ͯ�����ض�ͯ������������10������3�����Ƹ���Сѧ���й���540�����ض�ͯ��
��������
��1��������7�����ض�ͯ�༶��2������ռ�İٷֱ���12.5%��������ð༶���ܸ�����
��2������ƽ�����ļ��㹫ʽ���ÿ������ض�ͯ����Ȼ����������Ķ��������dz��ִ���������ȷ�����ض�ͯ��������
��3�����ð༶��60���ԣ�2������õ�ƽ����������
��1����У�İ༶������2��12.5%=16��������
��������8���İ༶������16��1��2��6��2=5��������
 ��
��
��2��ÿ������ض�ͯ��ƽ��������![]() ��1��6+2��7+5��8+6��10+12��2��=9���ˣ���������10����
��1��6+2��7+5��8+6��10+12��2��=9���ˣ���������10����
��3������Сѧ�������������ض�ͯ��60��9=540���ˣ���
��������Сѧ���й������ض�ͯ540����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ABC�У�D�DZ�BC�ϵ�һ�㣬��֪AC=5��AD=6��BD=10��CD=5����ô������ABC������ǣ�������
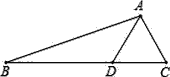
A. 30 B. 36 C. 72 D. 125
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУ����չ����������������������������������Ŀ������ƹ�����������ë��Ҫ��ÿλѧ��������ֻ��ѡ��һ�Ϊ�˽�ѡ������������Ŀ��ѧ�������������ȡ�˲���ѧ�����е��飬����ͨ�������õ����ݽ������������Ƴ�����������������ͳ��ͼ�������ͳ��ͼ�ش����⣺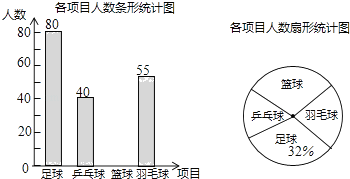
��1����λһ����������ѧ����
��2����ȫ����ͳ��ͼ��
��3��������ͳ��ͼ�У�ѡ��������Ŀ�������������ε�Բ�Ľǵ����ȣ�
��4������ѧУ��1500�ˣ�������Ƹ�ѧУѡ��������Ŀ��ѧ������Լ���ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����11�֣���Ȫͬѧ�μ���ĩ���ʵ������������ֻ������߲˴������ռ���20������������С�������ĸ�����32 39 45 55 60 54 60 28 56 41 51 36 44 46 40 53 37 47 45 46
��1��ǰ10������������С������������ƽ������ ����λ���� �������� ��
��2��������20���������8���з��飬�벹ȫƵ���ֲ�����Ƶ���ֲ�ֱ��ͼ��
�������� | 28��x��36 | 36��x��44 | 44��x��52 | 52��x��60 | 60��x��68 |
Ƶ�� | 2 | 2 |
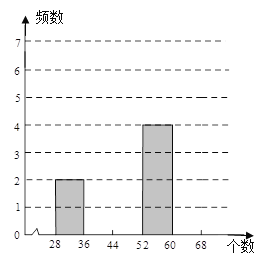
��3��ͨ��Ƶ���ֲ�ֱ��ͼ�Է����˴������������ij��ơ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
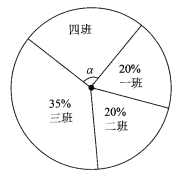
����Ŀ��Ϊ��ӭ�����й�������ʮ���꣬ij��ѧ���꼶��֯�ˡ���������ġ����ı��������յ�һ�ࡢ���ࡢ���ࡢ�İ����ѧ�������¹�100ƪ(����ѧ��ÿ��ֻ��һƪ)����������ͳ��ͼ�����˸������ѧ��ռ�������İٷֱ����(�в�����)������һ�����Ƚ����ɣ����ȫ�꼶25�˻������������ѧ���Ļ���Ϊ20����һ�����������İ�������ı�Ϊ6��7��a��5��
(1)��գ����İ���______�˲���������______�㣮
��a��______�������ѧ������������______��
(2)��һ�Ƚ������Ƚ���ѧ��ÿ�˷ֱ�õ���ֵ100Ԫ��60Ԫ��ѧϰ��Ʒ������������Ʒ����ȥ1900Ԫ����һ�Ƚ������Ƚ���ѧ�������ֱ��Ƕ���?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����������ABCD����࣬�������ȱ�������ADE��DCF������AF��BE
��1�����жϣ�AF��BE��������ϵ�� �� λ�ù�ϵ�� .
��2����ͼ2�����������������ȱ�������ADE��DCF����Ϊ����������������ADE��DCF����EA=ED=FD=FC�����ڣ�1�����еĽ����Ƿ���Ȼ�������������жϲ�����˵��
��3����������ADE��DCFΪһ�������Σ���AE=DF��ED=FC���ڣ�1�����еĽ��۶��ܳ�������ֱ��д������ж�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
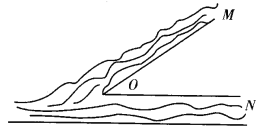
����Ŀ����������С��MO��NO��O����ϣ���ͼ��ʾ�������γɵ�ƽ����Ҫ��һ��С�ٻ��꣬ʹС�ٻ��굽�����߾�����ȣ������ӽ��㴦����300�ף��ٻ����λ�ø�����ȷ�������㰴10000��1�ı�������ͼ��ȷ���ٻ����λ�ã�������һ�£������ӱߵľ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ĶԽ����ཻ�ڵ�O����M��N�ֱ��DZ�BC��CD�ϵĶ��㣨�����B��C��D�غϣ���AM��AN�ֱ�BD�ڵ�E��F���ҡ�MANʼ�ձ���45�㲻�䣮
��1����֤�� ![]() =
= ![]() ��
��
��2����֤��AF��FM��
��3����̽�����ڡ�MAN����ת�����У�����BAM���ڶ��ٶ�ʱ����FMN=��BAM��д�����̽�����ۣ�������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ���ı���ABCD�У���ABC=60�㣬��E��F�ֱ���CD��BC���ӳ����ϣ�AE��BD��EF��BC��CF= ![]() ��
�� 
��1����֤���ı���ABDE��ƽ���ı��Σ�
��2����AB�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com