
分析 (1)先求出△=4(m2+3m),再分△=0,△>0,△<0三种情况讨论即可;
(2)先求出顶点P的坐标,根据题意得出方程,解方程即可.
解答 解:(1)y=x2+2(m+1)x-m+1,
△=[2(m+1)]2-4(-m+1)
=4m2+8m+4+4m-4
=4(m2+3m),
当m=0,或m=-3时,△=0,抛物线与x轴有一个交点;
当m>0或m<-3时,△>0,抛物线与x轴有两个交点;
当-3<m<0时,△<0,抛物线与x轴没有交点;
综上所述:抛物线与x轴有1个或2个或没有交点;
故答案为:1或2或没有;
(2)抛物线y=x2+2(m+1)x-m+1的顶点P坐标为:(-m-1,-m2-3m),
∵点P在直线y=x+1上,
∴-m2-3m=-m-1+1,
解得:m=0,或m=-2,
∴当直线y=x+1经过二次函数y=x2+2(m+1)x-m+1图象的顶点P时,m的值是-2或0.
故答案为:-2或0.
点评 此题主要考查了抛物线与x轴交点的三种情况、字母系数的求法、解方程;熟练掌握抛物线与x轴的交点情况是解决问题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 己知,如图,矩形ABCD中,AD=3,DC=4,矩形EFGH的三个顶点E.G、H分别在矩形ABCD的边ABCD的边AB、CD、DA上,AH=1,连接CF.
己知,如图,矩形ABCD中,AD=3,DC=4,矩形EFGH的三个顶点E.G、H分别在矩形ABCD的边ABCD的边AB、CD、DA上,AH=1,连接CF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
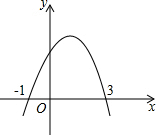 如图,抛物线y=ax2+bx+c交x轴于(-1,0)、(3,0)两点,则下列判断中,正确的是( )
如图,抛物线y=ax2+bx+c交x轴于(-1,0)、(3,0)两点,则下列判断中,正确的是( )| A. | ①② | B. | ①②④ | C. | ①②③ | D. | ④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| x | … | -1 | 0 | 1 | 2 | … |
| y | … | -1 | -$\frac{7}{4}$ | -2 | -$\frac{7}{4}$ | … |
| A. | 只有一个交点 | B. | 有两个交点,且它们均在y轴同侧 | ||
| C. | 无交点 | D. | 有两个交点,且它们分别在y轴两侧 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知抛物线y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2与x轴交于点A、B(点A在B的左侧),与y轴交于点C,若点F是直线BC上方的抛物线上一动点,是否存在点F,使△BCF的面积最大?若存在,求出定F的坐标;若不存在,请说明理由.
如图,已知抛物线y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2与x轴交于点A、B(点A在B的左侧),与y轴交于点C,若点F是直线BC上方的抛物线上一动点,是否存在点F,使△BCF的面积最大?若存在,求出定F的坐标;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 周末,东东一家三口人开车去距家15km的二克山公园游玩,行驶10min后,接到爷爷奶奶的电话,也要一同前往,于是妈妈下午步行前往,东东和爸爸开车按原路返回接爷爷奶奶,接到爷爷奶奶后,开车前往公园,在距离公园3.75km处追上妈妈并同车前往公园,若汽车速度始终保持不变,设汽车与家相距y1(单位:km),妈妈与家相距y2(单位:km),汽车离开家的时间为x(单位:min),y1、y2与x之间的函数图象如图所示,结合图象解答下列问题:
周末,东东一家三口人开车去距家15km的二克山公园游玩,行驶10min后,接到爷爷奶奶的电话,也要一同前往,于是妈妈下午步行前往,东东和爸爸开车按原路返回接爷爷奶奶,接到爷爷奶奶后,开车前往公园,在距离公园3.75km处追上妈妈并同车前往公园,若汽车速度始终保持不变,设汽车与家相距y1(单位:km),妈妈与家相距y2(单位:km),汽车离开家的时间为x(单位:min),y1、y2与x之间的函数图象如图所示,结合图象解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
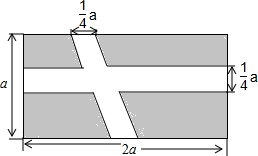 小林负责一块宽为a,长为2a的长方形草坪铺设鹅卵石小路供游人行走,他计划铺设两条宽为$\frac{1}{4}$a的鹅卵石(如图所示),其余部分全部种草
小林负责一块宽为a,长为2a的长方形草坪铺设鹅卵石小路供游人行走,他计划铺设两条宽为$\frac{1}{4}$a的鹅卵石(如图所示),其余部分全部种草查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com