
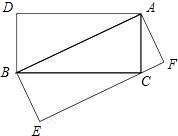
 解:(1)如果一个三角形和一个平行四边形满足条件:三角形的一边与平行四边形的一边重合,三角形这边所对的顶点在平行四边形这边的对边上,则称这样的平行四边形为三角形的“友好平行四边形”.
解:(1)如果一个三角形和一个平行四边形满足条件:三角形的一边与平行四边形的一边重合,三角形这边所对的顶点在平行四边形这边的对边上,则称这样的平行四边形为三角形的“友好平行四边形”. 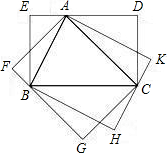
| 2S |
| a |
| 2S |
| b |
| 2S |
| c |
| 2S |
| a |
| 2S |
| b |
| 2s |
| ab |
| ab-S |
| ab |


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:阅读理解
阅读以下短文,然后解决下列问题:
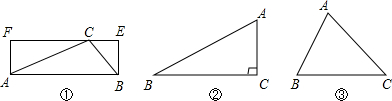
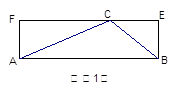
如果一个三角形和一个矩形满足条件:三角形的一边与矩形的一边重合,且三角形的这边所对的顶点在矩形这边的对边上,则称这样的矩形为三角形的“友好矩形”。如图(1)所示,矩形ABEF即为△ABC的“友好矩形”。显然,当△ABC是钝角三角形时,其“友好矩形”只有一个。
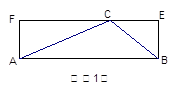
1.仿照以上叙述,说明什么是一个三角形的“友好平行四边形”
2.如图(2),若△ABC为直角三角形,且∠C=90°,在图(2)
中画出△ABC的所有“友好矩形”,并比较这些矩形面积的大小;
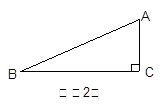
3.若△ABC是锐角三角形,且BC>AC>AB,在图(3)中画出△ABC的所有“友好矩形”,指出其中周长最大的矩形。(标上字母)
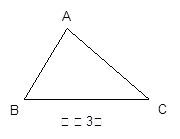
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解

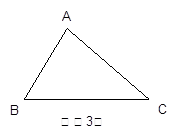
查看答案和解析>>
科目:初中数学 来源:2011-2012学年浙江杭州萧山瓜沥片八年级第二学期5月月考数学试卷(带解析) 题型:解答题
阅读以下短文,然后解决下列问题:
如果一个三角形和一个矩形满足条件:三角形的一边与矩形的一边重合,且三角形的这边所对的顶点在矩形这边的对边上,则称这样的矩形为三角形的“友好矩形”。如图(1)所示,矩形ABEF即为△ABC的“友好矩形”。显然,当△ABC是钝角三角形时,其“友好矩形”只有一个。
【小题1】仿照以上叙述,说明什么是一个三角形的“友好平行四边形”
【小题2】如图(2),若△ABC为直角三角形,且∠C=90°,在图(2)
中画出△ABC的所有“友好矩形”,并比较这些矩形面积的大小;
【小题3】若△ABC是锐角三角形,且BC>AC>AB,在图(3)中画出△ABC的所有“友好矩形”,指出其中周长最大的矩形。(标上字母)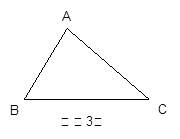
查看答案和解析>>
科目:初中数学 来源:2013届浙江杭州萧山瓜沥片八年级第二学期5月月考数学试卷(解析版) 题型:解答题
阅读以下短文,然后解决下列问题:
如果一个三角形和一个矩形满足条件:三角形的一边与矩形的一边重合,且三角形的这边所对的顶点在矩形这边的对边上,则称这样的矩形为三角形的“友好矩形”。如图(1)所示,矩形ABEF即为△ABC的“友好矩形”。显然,当△ABC是钝角三角形时,其“友好矩形”只有一个。

1.仿照以上叙述,说明什么是一个三角形的“友好平行四边形”
2.如图(2),若△ABC为直角三角形,且∠C=90°,在图(2)
中画出△ABC的所有“友好矩形”,并比较这些矩形面积的大小;
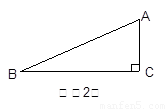
3.若△ABC是锐角三角形,且BC>AC>AB,在图(3)中画出△ABC的所有“友好矩形”,指出其中周长最大的矩形。(标上字母)
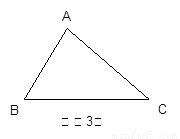
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com