
 如图.在矩形ABCD中.AB=6.BC=8.点A在直线1上,AD与直线1相交所得的锐角为60°,点F在直线1上.AF=8.EF⊥直线1.垂足为点F.且EF=6.以EF为直径.在EF的左侧作半圆O.点M是半圆O上任一点.
如图.在矩形ABCD中.AB=6.BC=8.点A在直线1上,AD与直线1相交所得的锐角为60°,点F在直线1上.AF=8.EF⊥直线1.垂足为点F.且EF=6.以EF为直径.在EF的左侧作半圆O.点M是半圆O上任一点.分析 发现:先依据勾股定理求得AO的长,然后由圆的性质可得到OM=3,当点M在AO上时,AM有最小值,当点M与点E重合时,AM有最大值,然后过点B作BG⊥l,垂足为G,接下来求得BG的长,从而可证明四边形OBGF为平行四边形,于是可得到OB与直线1的位置关系.
思考:连结OG,过点O作OH⊥EG,依据垂径定理可知GE=2HE,然后在△EOH中,依据特殊锐角三角函数值可求得HE的长,从而得到EG的长,接下来求得∠EOG得度数,依据弧长公式可求得弧EG的长;
探究:(1)如图3所示,连结OH,OA.先证明AO为∠DAF的角平分线,则∠OAF=30°,利用特殊锐角三角函数值可求得AF的长,从而可求得x的值;如图4所示:连结OH,OA,如图5所示:延长CB交FA与G,连结OH,OG,同理可求得x的值;(2)由(1)中相切的时x的值,并结合图形可得到半圆O与矩形ABCD的边有两个交点是x的取值范围.
解答 解:发现:由题意可知OM=OF=3,AF=8,EF⊥l,
∴OA=$\sqrt{A{F}^{2}+O{F}^{2}}$=$\sqrt{{8}^{2}+{3}^{2}}$=$\sqrt{73}$.
当点M在线段OA上时,AM有最小值,最小值为=$\sqrt{73}$-3.
当点M与点E重合时,AM有最大值,最大值=$\sqrt{A{F}^{2}+E{F}^{2}}$=10.
如图1所示:过点B作BG⊥l,垂足为G.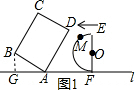
∵∠DAF=60°,∠BAD=90°,
∴∠BAG=30°.
∴GB=$\frac{1}{2}$AB=3.
∴OF=BG=3,
又∵GB∥OF,
∴四边形OBGF为平行四边形,
∴OB∥FG,即OB∥l.
故答案为:$\sqrt{73}$-3;10;平行.
思考:如图2所示:连结OG,过点O作OH⊥EG.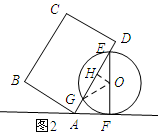
∵∠DAF=60°,EF⊥AF,
∴∠AEF=30°.
∴∠GOE=120°.
∴GE=2EH=2×$\frac{\sqrt{3}}{2}$×3=3$\sqrt{3}$.
弧EG的长=$\frac{120π×3}{180}$=2π.
∴半圆与矩形重合部分的周长=3$\sqrt{3}$+2π.
探究:(1)如图3所示,连结OH,OA.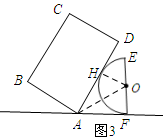
∵AD为圆O的切线,H为切点,
∴OH⊥AD.
又∵OF⊥AF,OH=OF,
∴AO为∠DAF的角平分线,
∴∠OAF=30°.
∴AF=$\sqrt{3}$OF=3$\sqrt{3}$.
∴x=8-3$\sqrt{3}$.
如图4所示:连结OH,OA.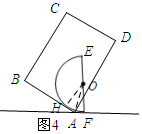
∵AH、AF均为圆O的切线,
∴OA为∠HAF的角平分线,
∴∠OAF=75°.
∴$\frac{AF}{OF}$=$\frac{1}{2+\sqrt{3}}$,即AF=6-3$\sqrt{3}$.
x=8-(6-3$\sqrt{3}$)=3$\sqrt{3}$+2.
如图5所示:延长CB交FA与G,连结OH,OG.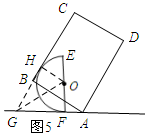
∵BC、FG为圆O的切线,
∴OG平分∠HGF,
∴∠OGF=30°.
∴AG=6÷$\frac{\sqrt{3}}{2}$=4$\sqrt{3}$,FG=3$\sqrt{3}$,
∴AF=$\sqrt{3}$.
∴x=8+$\sqrt{3}$.
综上所述,当x的值为8-3$\sqrt{3}$或3$\sqrt{3}$+2或8+$\sqrt{3}$时,半圆O与矩形ABCD的边相切.
(2)由(1)可知当8-3$\sqrt{3}$<x<3$\sqrt{3}$+2时,或8<x<8+$\sqrt{3}$时,半圆O与矩形ABCD的边有两个交点.
点评 本题主要考查的是圆的综合应用,解答本题主要应用了切线的性质和判定、特殊锐角三角函数值的应用、切线长定理,依据题意画出符合题意的图形是解题的关键.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:选择题
| A. | 不在同一条直线上的三个点确定一个圆 | |
| B. | 相等的圆心角所对的弧相等 | |
| C. | 平分弦的直径垂直于弦 | |
| D. | 在同圆或等圆中,相等的弦所对的圆周角相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
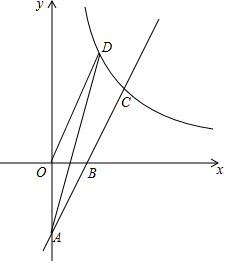 如图,在平面直角坐标系中,直线y=kx-4(k≠0)与坐标轴交于A、B两点,与反比例函数y=$\frac{m}{x}$(m≠0,x>0)在第一象限内的图象交于点C(4,a),反比例函数图象上有一点D(b,6),连接OD和AD,已知:tan∠OAB=$\frac{1}{2}$.
如图,在平面直角坐标系中,直线y=kx-4(k≠0)与坐标轴交于A、B两点,与反比例函数y=$\frac{m}{x}$(m≠0,x>0)在第一象限内的图象交于点C(4,a),反比例函数图象上有一点D(b,6),连接OD和AD,已知:tan∠OAB=$\frac{1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
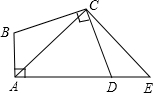 如图,在四边形ABCD中,∠A=∠BCD=90°,BC=CD.延长AD到E点,使DE=AB.
如图,在四边形ABCD中,∠A=∠BCD=90°,BC=CD.延长AD到E点,使DE=AB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com