
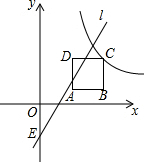
 边长为a的正方形ABCD在平面直角坐标系中的位置如图所示,其中AB与x轴平行(点B在点A的右侧),点A的坐标为(2,1),反比例函数y=$\frac{m}{x}$经过点C,直线l:y=kx-2(k≠0)与y轴交于点E.
边长为a的正方形ABCD在平面直角坐标系中的位置如图所示,其中AB与x轴平行(点B在点A的右侧),点A的坐标为(2,1),反比例函数y=$\frac{m}{x}$经过点C,直线l:y=kx-2(k≠0)与y轴交于点E.分析 (1)①先求出点C的坐标,用待定系数法即可得出结论;
②先根据正方形的性质,判断出直线l必过正方形的中心,再求出正方形的中心的坐标,用待定系数法即可得出结论;
(2)先表示出点C,D的坐标,进而得出CD的解析式,联立直线l的解析式求出点F的坐标,利用点F在线段CD和DF不超过3,建立不等式求解即可.
解答 解:(1)①∵四边形ABCD是边长为a的正方形,
∴AB=BC=2,
∵A(2,1),
∴B(4,1),D(2,3),
∴C(4,3),
∵反比例函数y=$\frac{m}{x}$经过点C,
∴m=4×3=12,
∴反比例函数的解析式为y=$\frac{12}{x}$;
②∵当直线l把正方形ABCD分为面积相等的两部分时,
∴直线l必过正方形ABCD的中心,
即:直线l过正方形ABCD的对角线BD的中点M(记:BD的中点为M),
由(1)知,B(4,1),D(2,3),
∴M(3,2),
∵直线l的解析式为y=kx-2,
∴2=3k-2,
∴k=$\frac{4}{3}$;
(2)∵正方形ABCD的边长为a,A(2,1),
∴B(a+2,1),D(2,a+1),
∴C(a+2,a+1),
∴直线CD的解析式为y=a+1①,
∵k=2,
∴直线l的解析式为y=2x-2②,
联立①②得,x=$\frac{1}{2}$(a-1),y=a+1,
∵F($\frac{1}{2}$(a-1),(a+1)),
∵点F在边CD上,
∴2≤$\frac{1}{2}$(a-1)≤a+2,
∴a≥5,
∵D(2,a+1),F($\frac{1}{2}$(a-1),(a+1)),
∴DF=$\frac{1}{2}$(a-1)-2=$\frac{1}{2}$a-$\frac{5}{2}$,
∵DF不超过3,
∴$\frac{1}{2}$a-$\frac{5}{2}$≤3,
∴a≤11,
∴5≤a≤11.
点评 此题是反比例函数综合题,主要考查了待定系数法,正方形的性质,解方程组,不等式,解(1)的关键是求出点C的坐标和,掌握正方形的性质,解(2)的关键是确定出点F的坐标,用方程或不等式的思想解决本题的难点,是一道中等难度的题目.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
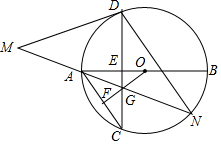 如图,已知⊙O的直径AB垂直于弦CD,垂足为E,点F为弦AC的中点,连接OF交CD于点G,直线AG交⊙O于点N,交过点D的⊙O的切线于点M,
如图,已知⊙O的直径AB垂直于弦CD,垂足为E,点F为弦AC的中点,连接OF交CD于点G,直线AG交⊙O于点N,交过点D的⊙O的切线于点M,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系中,我们不妨把横坐标与纵坐标相等的点称为梦之点,例如,点(1,1),(-2,-2),($\sqrt{2}$,$\sqrt{2}$),…,都是梦之点,显然梦之点有无数个.
在平面直角坐标系中,我们不妨把横坐标与纵坐标相等的点称为梦之点,例如,点(1,1),(-2,-2),($\sqrt{2}$,$\sqrt{2}$),…,都是梦之点,显然梦之点有无数个.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
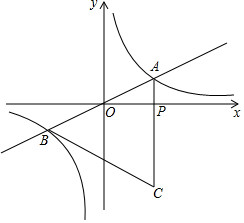 如图,直线y=kx与双曲线y=$\frac{\sqrt{3}}{x}$在一三象限分别交于A、B两点,等边△ABC的边AC交x轴于P点.
如图,直线y=kx与双曲线y=$\frac{\sqrt{3}}{x}$在一三象限分别交于A、B两点,等边△ABC的边AC交x轴于P点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6 | B. | 8 | C. | 10 | D. | 8或10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com