

分析 (1)根据姐妹抛物线的定义,可得答案;
(2)姐妹抛物线的定义,可得C2的顶点,C2余x轴的另一个交点,根据待定系数法,可得答案;
(3)根据二次函数的性质、矩形的性质,可得A,M点坐标,根据待定系数法,可得答案;再根据姐妹抛物线的定义,可得答案.
解答 解:(1)在抛物线C1:y=-x2+2x中,顶点A(1,1),与x轴的另一个交点M(2,0);
在抛物线C2:y=x+2x中,顶点B(-1,-1),与x轴的另一个交点N(-2,0);
∴A与B,M与N都关于原点O成中心对称,
∴抛物线C1:y=-x2+2x和C2:y=x2+2x是“姐妹抛物线”.
(2)抛物线C1:y=-3x2-4x的顶点A(-$\frac{2}{3}$,$\frac{4}{3}$),与x轴的另一个交点M(-$\frac{4}{3}$,0),
∴抛物线C2的顶点B($\frac{2}{3}$,-$\frac{4}{3}$),与x轴的另一个交点N($\frac{4}{3}$,0),
∴设抛物线C2为y=a(x-$\frac{2}{3}$)2-$\frac{4}{3}$,将N($\frac{4}{3}$,0)代入,得a($\frac{4}{3}$-$\frac{2}{3}$)2-$\frac{4}{3}$=0,解之,得a=3,
∴C2:y=3(x-$\frac{2}{3}$)2-$\frac{4}{3}$=3x2-4x.
(3)根据四边形ANBM恰好是矩形可得:OA=OM,
∵OA=MA,
∴△AOM是等边三角形,
设C1y=ax2+bx,
OM=2,则点A(1,$\sqrt{3}$),M(2,0),代入,得$\left\{\begin{array}{l}{a+b=\sqrt{3}}\\{4a+2b=0}\end{array}\right.$,解之,得$\left\{\begin{array}{l}{a=-\sqrt{3}}\\{b=2\sqrt{3}}\end{array}\right.$,
此时抛物线C1的表达式为y=-$\sqrt{3}$x2+2$\sqrt{3}$x,
C2的表达式为y=$\sqrt{3}$x2+2$\sqrt{3}$x,
故答案为y=-$\sqrt{3}$x22+2$\sqrt{3}$x,y=$\sqrt{3}$x2+2$\sqrt{3}$x.
点评 本题考查了二次函数综合题,解(1)的关键是利用姐妹抛物线的定义;解(2)的关键是利用姐妹抛物线的定义得出点B($\frac{2}{3}$,-$\frac{4}{3}$),与x轴的另一个交点N($\frac{4}{3}$,0),又利用了待定系数法;解(3)的关键是利用矩形的性质,二次函数的性质得出A,M的坐标,又利用了姐妹抛物线的定义.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
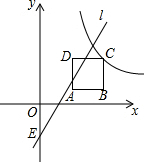 边长为a的正方形ABCD在平面直角坐标系中的位置如图所示,其中AB与x轴平行(点B在点A的右侧),点A的坐标为(2,1),反比例函数y=$\frac{m}{x}$经过点C,直线l:y=kx-2(k≠0)与y轴交于点E.
边长为a的正方形ABCD在平面直角坐标系中的位置如图所示,其中AB与x轴平行(点B在点A的右侧),点A的坐标为(2,1),反比例函数y=$\frac{m}{x}$经过点C,直线l:y=kx-2(k≠0)与y轴交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
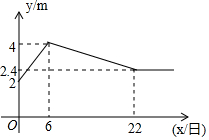 如图,是皖韵水库进入5月份以来的水位y米与x日的函数图象,为了避免过度捕捞,当水位低于3米时就不适宜渔船打捞作业,根据图象可知,5月份能打捞的天数有( )天.
如图,是皖韵水库进入5月份以来的水位y米与x日的函数图象,为了避免过度捕捞,当水位低于3米时就不适宜渔船打捞作业,根据图象可知,5月份能打捞的天数有( )天.| A. | 11 | B. | 12 | C. | 13 | D. | 14 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
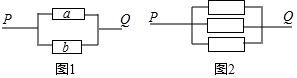 在物理实验中,当电流在一定时间段内正常通过电子元件时,每个电子元件的状态有两种可能;通电或断开,并且这种状态的可能性相等.
在物理实验中,当电流在一定时间段内正常通过电子元件时,每个电子元件的状态有两种可能;通电或断开,并且这种状态的可能性相等.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
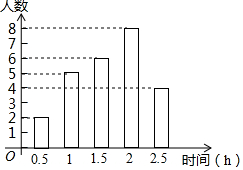 某班25名同学在一周内做家务劳动时间如图所示,则做家务劳动时间的众数和中位数分别是( )
某班25名同学在一周内做家务劳动时间如图所示,则做家务劳动时间的众数和中位数分别是( )| A. | 2和1.5 | B. | 1.5和1.5 | C. | 2和2.5 | D. | 1.75和2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m<1 | B. | m≤1 | C. | m<1且m≠0 | D. | m≤1且m≠0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
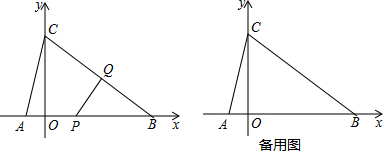
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
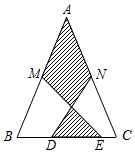 如图,在△ABC中,AB=AC,M,N分别是AB,AC的中点,D,E为BC上的点,连结DN,EM.若AB=13cm,BC=10cm,DE=5cm,则图中阴影部分面积为( )cm2.
如图,在△ABC中,AB=AC,M,N分别是AB,AC的中点,D,E为BC上的点,连结DN,EM.若AB=13cm,BC=10cm,DE=5cm,则图中阴影部分面积为( )cm2.| A. | 25 | B. | 35 | C. | 30 | D. | 42 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com