
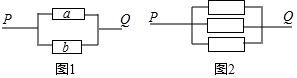 在物理实验中,当电流在一定时间段内正常通过电子元件时,每个电子元件的状态有两种可能;通电或断开,并且这种状态的可能性相等.
在物理实验中,当电流在一定时间段内正常通过电子元件时,每个电子元件的状态有两种可能;通电或断开,并且这种状态的可能性相等.分析 (1)根据题意列出表格或画出树状图,即可求得所有等可能的结果与P、Q之间电流通过的情况,继而利用概率公式求解解即可求得答案;
(2)根据题意画出树状图,即可求得所有等可能的结果与P、Q之间电流通过的情况,继而利用概率公式求解解即可求得答案.
解答 解:(1)用树状图表示为: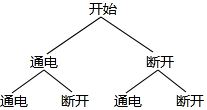
则P、Q之间电流通过的概率$\frac{3}{4}$;
(2)画树状图得: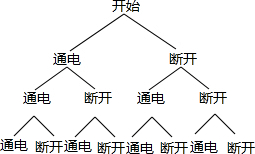
则P、Q之间电流通过的概率是$\frac{7}{8}$.
点评 此题考查了树状图法与列表法求概率.注意列表法与树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;注意概率=所求情况数与总情况数之比.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1>y2>0 | B. | y2>y1>0 | C. | 0>y1>y2 | D. | 0>y2>y1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
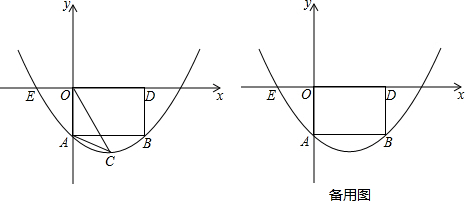
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | $\frac{16}{3}$ | C. | 6 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
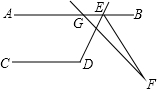 如图,已知AB∥CD,∠CDE=118°,直线GF与AB交于点G,与∠BED的平分线交于点F,若∠AGF=132°,则∠F的度数为( )
如图,已知AB∥CD,∠CDE=118°,直线GF与AB交于点G,与∠BED的平分线交于点F,若∠AGF=132°,则∠F的度数为( )| A. | 24° | B. | 12° | C. | 11° | D. | 10° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com