
(2011•雅安)如图,在△ABC中,AB=AC,以AB为直径作⊙O,交BC于点D,过点D作DE⊥AC,垂足为E.
(1)求证:DE是⊙O的切线;
(2)如果BC=8,AB=5,求CE的长.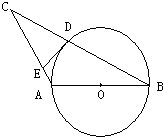
解:(1)证明:连接OD.
∵OD=OB?(⊙O的半径),
∴∠B=∠ODB(等边对等角);
∵AB=AC(已知),
∴∠B=∠C(等边对等角);
∴∠C=∠ODB(等量代换),
∴OD∥AC(同位角相等,两直线平行),
∴∠ODE=∠DEC(两直线平行,内错角相等);
∵DE⊥AC(已知),
∴∠DEC=90°,
∴∠ODE=90°,即DE⊥OD,
∴DE是⊙O的切线;
(2)连接AD.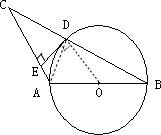
∵AB是⊙O的直径,
∴∠ADB=90°(直径所对的圆周角是直角);
∴AD⊥CD;
在Rt△ACD和Rt△DCE中,
∠C=∠C(公共角),
∠CED=∠CDA=90°,
∴Rt△ACD∽Rt△DCE(AA),
∴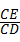 =
= ;
;
又由(1)知,OD∥AC,O是AB的中点,
∴OD是三角形ABC的中位线,
∴CD=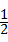 BC;
BC;
∵BC=8,AB=5,AB=AC,
∴CE=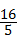 .
.
解析


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
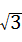 ,求证:四边形AECF是菱形.
,求证:四边形AECF是菱形.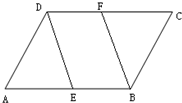
查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(四川攀枝花卷)数学解析版 题型:解答题
(2011•雅安)如图,在?ABCD中,E,F分别是BC,AD中点.
(1)求证:△ABE≌△CDF;
(2)当BC=2AB=4,且△ABE的面积为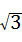 ,求证:四边形AECF是菱形.
,求证:四边形AECF是菱形.
查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(四川攀枝花卷)数学解析版 题型:填空题
(2011•雅安)如图,在平面直角坐标系中,菱形OABC的顶点B的坐标为(8,4),则C点的坐标为 .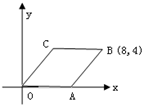
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com