练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    2．为了解某社区居民的用电情况，随机对该社区10户居民进行调查，表是这l0户居民2016年4月份用电量的调查结果：
    居民1234
    月用电量（度/户）304250
    那么关于这10户居民月用电量（单位：度），下列说法错误的是（　　）
    A．中位数是50B．众数是51C．方差是42D．平均数为46.8

    分析 根据表格中的数据，求出平均数，中位数，众数，极差与方差，即可做出判断．

    解答 解：10户居民2015年4月份用电量为30，42，42，50，50，50，51，51，51，51，
    中位数为50；众数为51，平均数为$\frac{1}{10}$（30+42+42+50+50+50+51+51+51+51）=46.8，
    方差为$\frac{1}{10}$[（30-46.8）2+2（42-46.8）2+3（50-46.8）2+4（51-46.8）2]=42.96，
    故选：C．

    点评 此题考查了方差，中位数，众数，以及极差，熟练掌握各自的求法是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

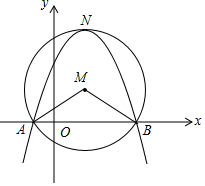    4．如图，在平面直角坐标系中，O是原点，以点M（2，2）为圆心，4为半径作圆，交x轴于A，B两点，开口向下的抛物线经过点A，B，且其顶点N在⊙M上．
    （1）点A坐标（2-2$\sqrt{3}$，0），点B坐标（2+2$\sqrt{3}$，0）；
    （2）求抛物线的解析式；
    （3）点P（m，n）在直线y=-x+$\frac{13}{2}$上方的抛物线上，且∠APB＞60°，求m的取值范围；
    （4）在该抛物线上是否存在一点D，使线段ON与MD互相平分？若存在，求出点D的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

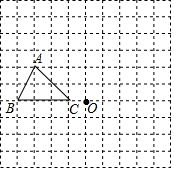    13．在如图的方格纸中，每个小方格都是边长为1个单位的正方形，△ABC顶点都在格点上（每个小方格的顶点叫格点）．
    （1）画出△ABC向上平移4个单位后的△A1B1C1；
    （2）画出△ABC绕点O顺时针旋转90°后的△A2B2C2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．一个不透明的口袋里装有分别标有汉字“喜”、“迎”、“峰”、“会”的四个小球，除汉字不同之外，小球没有任何区别，每次摸球前先搅拌均匀再摸球．
    （1）若从中任取一个球，求球上的汉字刚好是“峰”的概率；
    （2）从中任取一球，不放回，再从中任取一球，请用树状图或列表法，求取出的两个球上的汉字恰能组成“喜迎”或“峰会”的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．把下列各数分别填入相应的集合里．
    -5，|-$\frac{3}{4}}$|，0，-3.14，$\frac{22}{7}$，-12，0.1010010001…，+1.99，-（-6），-$\frac{π}{3}$
    （1）无理数集合：{                                                 …}
    （2）正数集合：{                                                   …}
    （3）整数集合：{                                                   …}
    （4）分数集合：{                                                   …}．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．如图1，在四边形ABCD中，BC∥AD，∠B=90°，AD边落在平面直角坐标系的x轴上，且点A（5，0）、D（3，0），点C坐标为（0，3）．点P从点E（-5，0）出发，沿x轴向点A以每秒1个单位长度的速度运动，到达点A时停止运动．运动时间为t秒．
    （1）点B的坐标为（5，3）；
    （2）当t=2，5，2+3$\sqrt{2}$时，△PCD为等腰三角形；
    （3）如图2，以点P为圆心，PC为半径作⊙P．
    ①求当t为何值时，⊙P与四边形ABCD的一边（或边所在的直线）相切；
    ②若⊙P与四边形ABCD的交点有两个，请直接写出运动时间t的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．选择适当的方法解方程：
    （1）2（x-3）=3x（x-3）．
    （2）2x2-3x+1=0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

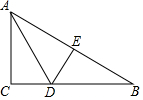    11．如图，△ABC中∠C=90°，线段AD是△ABC的角平分线，直线DE是线段AB的垂直平分线．若DE=1cm，DB=2cm，AC=$\sqrt{3}$cm．求点C到直线AD的距离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

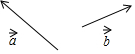    12．如图，已知两个不平行的向量$\overrightarrow{a}$与$\overrightarrow{b}$，先化简，再求作：（3$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$）-（2$\overrightarrow{a}$-$\frac{3}{2}$$\overrightarrow{b}$）．

    查看答案和解析>>

    同步练习册答案