
 ∠OAB=2。
∠OAB=2。
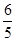 ,-
,-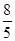 ),使ΔAPC与ΔAOB相似。
),使ΔAPC与ΔAOB相似。 ∠OAB=
∠OAB=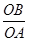
 ∠OAB=2
∠OAB=2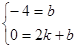 ∴
∴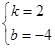

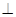 AB交AB于P2,过P2作P1D
AB交AB于P2,过P2作P1D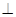 AC于D
AC于D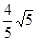
 ∴OD=
∴OD=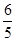 ,
,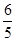 时,y=-
时,y=-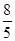
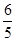 ,-
,-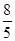 )
)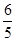 ,-
,-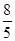 ),使ΔAPC与ΔAOB相似
),使ΔAPC与ΔAOB相似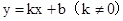 。求直线解析式时需要具备2个已知点坐标,为解题关键。题(3)中求证点P是否存在使两三角形相似。通过证相似三角形的判定定理我们可知必然需要得到两三角形对应角相等或者对应边比值相等的条件才能证相似。那么假设存在该点P使形成的三角形与已知的直角三角形相似,通过做辅助垂线,构成两组对应角相等是解题关键,然后得到两个P点,并通过点P在直线AB上,用直线AB解析式求出点P坐标。
。求直线解析式时需要具备2个已知点坐标,为解题关键。题(3)中求证点P是否存在使两三角形相似。通过证相似三角形的判定定理我们可知必然需要得到两三角形对应角相等或者对应边比值相等的条件才能证相似。那么假设存在该点P使形成的三角形与已知的直角三角形相似,通过做辅助垂线,构成两组对应角相等是解题关键,然后得到两个P点,并通过点P在直线AB上,用直线AB解析式求出点P坐标。

 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
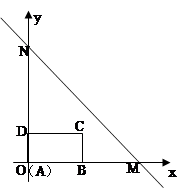
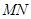 :
: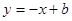 与
与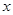 轴交于点
轴交于点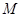 (4,0),与
(4,0),与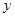 轴交于点
轴交于点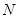 ,长方形
,长方形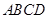 的边
的边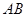 在
在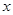 轴上,
轴上,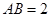 ,
,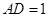 .长方形
.长方形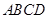 由点
由点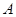 与点
与点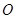 重合的位置开始,以每秒1个单位长度的速度沿
重合的位置开始,以每秒1个单位长度的速度沿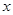 轴正方向作匀速直线运动,当点
轴正方向作匀速直线运动,当点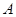 与点
与点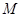 重合时停止运动.设长方形运动的时间为
重合时停止运动.设长方形运动的时间为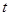 秒,长方形
秒,长方形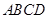 与△
与△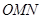 重合部分的面积为
重合部分的面积为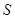 .
.
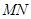 的解析式;
的解析式;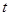 =1时,请判断点
=1时,请判断点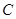 是否在直线
是否在直线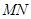 上,并说明理由;
上,并说明理由; 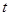 为何值时,点
为何值时,点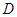 在直线
在直线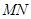 上;
上;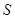 与
与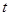 的函数关系式.
的函数关系式.查看答案和解析>>
科目:初中数学 来源:不详 题型:计算题
 种布料
种布料 ,
, 种布料
种布料 ,现计划用这两种布料生产
,现计划用这两种布料生产  、
、 两种型号的时装共
两种型号的时装共 套。已知做一套
套。已知做一套 型号的时装需用
型号的时装需用 种布料
种布料 ,
, 种布料
种布料 ,可获利润
,可获利润 元;做一套
元;做一套 型号的时装需用
型号的时装需用 种布料
种布料 ,
, 种布料
种布料 ,可获利润
,可获利润 元。若设生产
元。若设生产 型号的时装套数为
型号的时装套数为 ,用这批布料生产这两种型号的时装所获得的总利润为
,用这批布料生产这两种型号的时装所获得的总利润为 元。
元。 (元)与
(元)与 (套)的函数关系,利用一次函数性质,选出(1)中哪个方案所获利润最大?最大利润是多少?
(套)的函数关系,利用一次函数性质,选出(1)中哪个方案所获利润最大?最大利润是多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com