
(本小题满分12分)
如图,在平面直角坐标系中,顶点为( ,
, )的抛物线交
)的抛物线交 轴于
轴于 点,交
点,交 轴于
轴于 ,
, 两点(点
两点(点 在点
在点 的左侧), 已知
的左侧), 已知 点坐标为(
点坐标为( ,
, )。
)。
(1)求此抛物线的解析式;
(2)过点 作线段
作线段 的垂线交抛物线于点
的垂线交抛物线于点 , 如果以点
, 如果以点 为圆心的圆与直线
为圆心的圆与直线 相切,请判断抛物线的对称轴
相切,请判断抛物线的对称轴 与⊙
与⊙ 有怎样的位置关系,并给出证明;
有怎样的位置关系,并给出证明;
 (3)已知点
(3)已知点 是抛物线上的一个动点,且位于
是抛物线上的一个动点,且位于 ,
, 两点之间,问:当点
两点之间,问:当点 运动到什么位置时,
运动到什么位置时, 的面积最大?并求出此时
的面积最大?并求出此时 点的坐标和
点的坐标和 的最大面积.
的最大面积.
(1)设抛物线为 .
.
∵抛物线经过点 (0,3),∴
(0,3),∴ .∴
.∴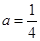 .
.
∴抛物线为 . ……………………………3分
. ……………………………3分
(2) 答: 与⊙
与⊙ 相交 …………………………………………………………………1分
相交 …………………………………………………………………1分
证明:当 时,
时, ,
, .
.
∴ 为(2,0),
为(2,0), 为(6,0).∴
为(6,0).∴ .…………………1分
.…………………1分
设⊙ 与
与 相切于点
相切于点 ,连接
,连接 ,则
,则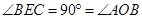 .
.
∵ ,∴
,∴ .
.
又∵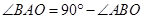 ,∴
,∴ .∴
.∴ ∽
∽ .……1分
.……1分
∴ .∴
.∴ .∴
.∴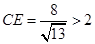 .…………………………1分
.…………………………1分
∵抛物线的对称轴 为
为 ,∴
,∴ 点到
点到 的距离为2.
的距离为2.
∴抛物线的对称轴 与⊙
与⊙ 相交. ……………………………………………1分
相交. ……………………………………………1分
解:如图,过点 作平行于
作平行于 轴的直线交
轴的直线交 于点
于点 。
。
可求出 的解析式为
的解析式为 .…………………………………………1分
.…………………………………………1分
设 点的坐标为(
点的坐标为( ,
, ),则
),则 点的坐标为(
点的坐标为( ,
, ).
).
∴ .
.
∵ ,
,
∴当 时,
时, 的面积最大为
的面积最大为 .
.
此时, 点的坐标为(3,
点的坐标为(3, ). …………………………………………3分
). …………………………………………3分
 |
【解析】略


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2011-2012学年九年级第二次模拟考试数学卷 题型:解答题
(本小题满分12分)
如图,反比例函数 的图象经过A、B两点,根据图中信息解答下列问题:
的图象经过A、B两点,根据图中信息解答下列问题:

1.(1)写出A点的坐标;
2.(2)求反比例函数的解析式;
3.(3)若点A绕坐标原点O旋转90°后得到点C,请写出点C的坐标;并求出直线BC的解析式.
查看答案和解析>>
科目:初中数学 来源:2011-2012年河北省衡水市五校九年级第三次联考数学卷 题型:解答题
(本小题满分12分)
如图(1),△ABC与△EFD为等腰直角三角形,AC与DE重合,AB=EF=9,∠BAC=∠DEF=90°,固定△ABC,将△EFD绕点A 顺时针旋转,当DF边与AB边重合时,旋转中止。不考虑旋转开始和结束时重合的情况,设DE、DF(或它们的延长线)分别交BC(或它的延长线)于G、H点,如图(2)。

1.(1)问:始终与△AGC相似的三角形有 及 ;
2.(2)设CG=x,BH=y,求y关于x的函数关系式(只要求根据2的情况说明理由);
3.(3)问:当x为何值时,△AGH是等腰三角形?
查看答案和解析>>
科目:初中数学 来源:2011-2012年河北省衡水市五校九年级第三次联考数学卷 题型:解答题
(本小题满分12分)某班同学到野外活动,为测量一池塘两端A、B的距离,设计了几种方案,下面介绍两种:(I)如图(1),先在平地取一个可以直接到达A、B的点C,并分别延长AC到D,BC到E,使DC=AC,BC=EC,最后测出DE的距离即为AB的长。(II)如图(2),先过B点作AB的垂线BF,再在BF上取C、D两点,使BC=CD,接着过点D作BD的垂线DE,交AC的延长线于E,则测出DE的长即为AB的距离。阅读后回答下列问题:

1.(1)方案(I)是否可行?为什么?
2.(2)方案(II)是否切实可行?为什么?
3.(3)方案(II)中作BF⊥AB,ED⊥BF的目的是 ;若仅满足∠ABD=∠BDE≠90°,方案(II)是否成立?
4.(4)方案(II)中,若使BC=n·CD,能否测得(或求出)AB的长?理由是 ,若ED=m,则AB= 。
查看答案和解析>>
科目:初中数学 来源:2011-2012年江苏GSJY八年级第二次学情调研考试数学卷 题型:解答题
(本小题满分12分)
1. (1)观察发现
如(a)图,若点A,B在直线 同侧,在直线
同侧,在直线 上找一点P,使AP+BP的值最小.
上找一点P,使AP+BP的值最小.
做法如下:作点B关于直线 的对称点
的对称点 ,连接
,连接 ,与直线
,与直线 的交点就是所求的点P
的交点就是所求的点P
再如(b)图,在等边三角形ABC中,AB=2,点E是AB的中点,AD是高,在AD上找一点P,使BP+PE的值最小.
做法如下:作点B关于AD的对称点,恰好与点C重合,连接CE交AD于一点,则这点就是所求的点P,故BP+PE的最小值为 . (2分)

2.(2)实践运用
如图,菱形ABCD的两条对角线分别长6和8,点P是对角线AC上的一个动点,点M、N分别是边AB、BC的中点,求PM+PN的最小值。(5分)

3.(3)拓展延伸
如(d)图,在四边形ABCD的对角线AC上找一点P,使∠APB=∠APD.保留作图痕迹,不必写出作法. (5分)

查看答案和解析>>
科目:初中数学 来源:2014届湖北省孝感市七年级下学期期中考试数学卷 题型:解答题
.(本小题满分12分)
如图,AD为△ABC的中线,BE为△ABD的中线。

(1)∠ABE=15°,∠BAD=40°,求∠BED的度数;
(2)在△BED中作BD边上的高;
(3)若△ABC的面积为40,BD=5,则△BDE 中BD边上的高为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com