
 如图,在△ABC中,∠C=90°,AB=5,BC=3,D是AB的中点,点E在边AC上,将△ADE沿DE翻折,使点A落在点A'处,当A'E⊥AC时,A'B=$\frac{\sqrt{2}}{2}$或$\frac{7}{2}\sqrt{2}$.
如图,在△ABC中,∠C=90°,AB=5,BC=3,D是AB的中点,点E在边AC上,将△ADE沿DE翻折,使点A落在点A'处,当A'E⊥AC时,A'B=$\frac{\sqrt{2}}{2}$或$\frac{7}{2}\sqrt{2}$. 分析 分两种情况进行讨论:①当A'在AC上方时,由折叠可得∠AED=∠A'ED,当A'E⊥AC时,∠AED=∠A'ED=45°,再过D作DF⊥AC于F,过B作BG⊥A'E于G,则△DEF是等腰直角三角形,再根据DF∥BC,D是AB的中点,BC=3,求得EF=$\frac{3}{2}$,CE=$\frac{1}{2}$,最后根据等腰Rt△A'BG中,A'B=$\sqrt{2}$BG,即可得到结论.②当A'在AC下方时,也是作辅助线构造等腰直角三角形和矩形,利用勾股定理进行计算求解.
解答 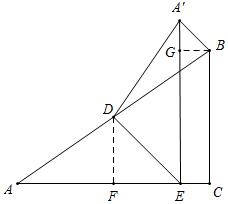 解:①如图所示,A'在AC上方,
解:①如图所示,A'在AC上方,
∵在△ABC中,∠C=90°,AB=5,BC=3,
∴AC=4,
由折叠可得∠AED=∠A'ED,
当A'E⊥AC时,∠AED=∠A'ED=45°,
如图,过D作DF⊥AC于F,过B作BG⊥A'E于G,则△DEF是等腰直角三角形,
∵DF∥BC,D是AB的中点,BC=3,
∴AF=CF=$\frac{1}{2}$AC=2,DF=$\frac{1}{2}$BC=$\frac{3}{2}$,
∴EF=$\frac{3}{2}$,CE=2-$\frac{3}{2}$=$\frac{1}{2}$,
∴矩形BCEG中,BG=CE=$\frac{1}{2}$,BC=EG=3,
∵AE=2+$\frac{3}{2}$=$\frac{7}{2}$,
∴A'E=$\frac{7}{2}$,
∴A'G=$\frac{7}{2}$-3=$\frac{1}{2}$,即A'G=BG,
∴等腰Rt△A'BG中,A'B=$\sqrt{2}$BG=$\frac{\sqrt{2}}{2}$.
②如图所示,A'在AC的下方,
由折叠可得∠AED=∠A'ED,
当A'E⊥AC时,∠AED=∠A'ED=135°,∠A'EF=90°,故∠DEF=45°,
过D作DF⊥AC于F,过A'作BG⊥BC于G,则△DEF是等腰直角三角形,
∴DF=EF=$\frac{1}{2}$BC=$\frac{3}{2}$,
又∵AF=$\frac{1}{2}$AC=2,
∴AE=$\frac{1}{2}$,EC=4-$\frac{1}{2}$=$\frac{7}{2}$=A'G,
又∵A'E=AE=$\frac{1}{2}$,
∴CG=$\frac{1}{2}$,
∴BG=BC+CG=$\frac{7}{2}$,即A'G=BG,
∴等腰Rt△A'BG中,A'B=$\sqrt{2}$BG=$\frac{7}{2}\sqrt{2}$,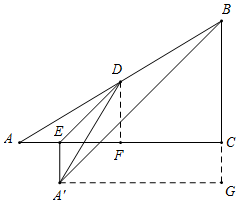
故答案为:$\frac{\sqrt{2}}{2}$或$\frac{7}{2}\sqrt{2}$.
点评 本题主要考查了折叠问题,等腰直角三角形的性质,矩形的性质,平行线分线段成比例定理以及勾股定理的综合应用,解题时注意:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,对应边和对应角相等.平行于三角形的一边,并且和其他两边相交的直线,所截得的三角形的三边与原三角形的三边对应成比例.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 时间t/天 | 1 | 3 | 6 | 10 | 36 | … |
| 日销售量m/件 | 94 | 90 | 84 | 76 | 24 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 问题探究:
问题探究:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一幅长20cm、宽12cm的图案,如图,其中有一横两竖的彩条,横、竖彩条的宽度比为3:2.若图案中三条彩条所占面积是图案面积的$\frac{2}{5}$,求横、竖彩条的宽度.
一幅长20cm、宽12cm的图案,如图,其中有一横两竖的彩条,横、竖彩条的宽度比为3:2.若图案中三条彩条所占面积是图案面积的$\frac{2}{5}$,求横、竖彩条的宽度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com