练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，已知在△ABC中，CD是AB边上的高线，BE平分∠ABC，交CD于点E，BC=5，DE=2，则△BCE的面积等于(     )

    A．10     B．7       C．5       D．4


    C【考点】角平分线的性质．

    【分析】作EF⊥BC于F，根据角平分线的性质求得EF=DE=2，然后根据三角形面积公式求得即可．

    【解答】解：作EF⊥BC于F，

    ∵BE平分∠ABC，ED⊥AB，EF⊥BC，

    ∴EF=DE=2，

    ∴S△BCE=BC•EF=×5×2=5，

    故选C．

    【点评】本题考查了角的平分线的性质以及三角形的面积，作出辅助线求得三角形的高是解题的关键．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    已知：∠AOB和两点C、D，求作一点P，使PC=PD，且点P到∠AOB的两边的距离相等．

    （要求：用尺规作图，保留作图痕迹，写出作法，不要求证明）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知一个等腰三角形的两边长分别是2和5，那么这个等腰三角形的周长为(     )

    A．9       B．12     C．9或12     D．7

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    ．1202班原有卫生区200平方米，现在由于某种原因变成了260平方米，因此要求搞卫生时每分钟比原来多搞15平方米，结果现在完成卫生任务的时间与原来的一样，求：

    （1）原来每分钟搞卫生多少平方米？

    （2）完成卫生任务要多少时间？

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知三角形的两边长是2cm，3cm，则该三角形的周长l的取值范围是(     )

    A．1＜l＜5    B．1＜l＜6    C．5＜l＜9    D．6＜l＜10

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    ．如图，AD是△ABC的角平分线，DE⊥AC，垂足为E，BF∥AC交ED的延长线于点F，若BC恰好平分∠ABF，AE=2BF．给出下列四个结论：①DE=DF；②DB=DC；③AD⊥BC；④AC=3BF，其中正确的结论共有(     )

    A．4个  B．3个   C．2个  D．1个

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，BD是∠ABC的平分线，DE∥CB，交AB于点E，∠A=45°，∠BDC=60°，求△BDE各内角的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    点M（﹣2，1）关于x轴对称的点N的坐标是__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图所示，在Rt△ABC中，AD是斜边上的高，∠ABC的平分线分别交AD、AC于点F、E，EG⊥BC于G，下列结论正确的是(     )

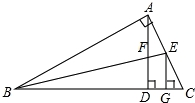
    A．∠C=∠ABC     B．BA=BG     C．AE=CE     D．AF=FD

    查看答案和解析>>

    同步练习册答案