Question

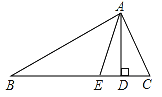
【题目】已知：如图，在△ABC中，AD、AE分别是△ABC的高和角平分线．

（1）若∠B=30°，∠C=50°，求∠DAE的度数．

（2）试问∠DAE与∠C﹣∠B有怎样的数量关系？说明理由．

Answer 1

【答案】（1）10°；（2）∠DAE=（∠C-∠B）.

【解析】试题分析：（1）先根据三角形内角和得到∠CAB=180°﹣∠B﹣∠C=100°，再根据角平分线与高线的定义得到∠CAE=∠CAB=50°，∠ADC=90°，则∠CAD=90°﹣∠C=40°，然后利用∠DAE=∠CAE﹣∠CAD计算即可．

（2）根据题意可以用∠B和∠C表示出∠CAD和∠CAE，从而可以得到∠DAE与∠C﹣∠B的关系．

试题解析：解：∵∠ABC=30°，∠ACB=50°，∴∠CAB=180°﹣∠B﹣∠C=100°，∵AE是△ABC角平分线，∴∠CAE=∠CAB=50°，∵AD是△ABC的高，∴∠ADC=90°，∴∠CAD=90°﹣∠C=40°，∴∠DAE=∠CAE﹣∠CAD=50°﹣40°=10°．

（2）∠DAE=（∠ACB﹣∠ABC），理由：∵在△ABC中，AD，AE分别是△ABC的高和角平分线，∴∠CAB=180°﹣∠B﹣∠C，∠CAD=90°﹣∠C，∠CAE=（180°﹣∠B﹣∠C），∴∠DAE=（180°﹣∠B﹣∠C）﹣（90°﹣∠C）=（∠C﹣∠B）．