
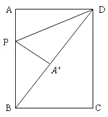
【题目】如图,矩形ABCD中,AB=8cm,BC=6cm,动点P从点A出发,以每秒1cm的速度沿线段AB向点B运动,连接DP,把∠A沿DP折叠,使点A落在点A′处.求出当△BPA′为直角三角形时,点P运动的时间.

【答案】答案见解析
【解析】整体分析:
因为不确定△BPA′的哪一个角是直角,所以需要分三种情况讨论,即(1)当∠BA′P=90°时;(2)当∠A′PB=90°时;(3)当∠A′BP=90°时,注意画出符合各种情况的图形,找出折叠后相等的边和角.
解:(1)当∠BA′P=90°时,由折叠得,∠PA′D=∠A=90°,
∴∠BA′D=∠BA′P+∠PA′D=180°,
∴点B、A′、D在一直线上,
Rt△ABD中,AD=6,AB=8,由勾股定理得BD=10.
设AP=xcm,
∴A′P=x,BP=8-x,A′B=10-6=4,
在Rt△A′PB中,x2+42=(8-x)2,
解得x=3.
∴点P运动的时间为3÷1=3秒.
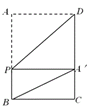
(2)当∠A′PB=90°时,∠A′PA=90°,
∵∠DA′P=90°,∴四边形APA′D是矩形,
∴A′P=AP,∴四边形APA′D是正方形,∴AP=AD=6,
∴点P运动的时间为6÷1=6秒.
(3)当∠A′BP=90°时,不存在.
综上所述,点P的运动时间为3s或6s.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=2 ![]() ,以点C为圆心,CB的长为半径画弧,与AB边交于点D,将
,以点C为圆心,CB的长为半径画弧,与AB边交于点D,将 ![]() 绕点D旋转180°后点B与点A恰好重合,则图中阴影部分的面积为
绕点D旋转180°后点B与点A恰好重合,则图中阴影部分的面积为 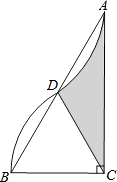
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划购买A、B两种品牌的显示器共120台,A、B两种品牌显示器的单价分别为800元和1000元,设购买A品牌显示器x台,若学校购买这两种品牌显示器的总费用为110000元,那么A、B两种品牌的显示器各购买了多少台?根据题目信息完成上面的表格,并列出方程,列出的方程: .
项目品牌 | 单价/元 | 购买数量/台 | 购买费用/元 |
A | 800 | x |
|
B | 1000 |
|
|
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(1,2),B(3,2),连接AB,点P是x轴上的一个动点,连接AP、BP,当△ABP的周长最小时,对应的点P的坐标和△ABP的最小周长分别为( )

A. (1,0), ![]() B. (3,0),
B. (3,0), ![]() C. (2,0),
C. (2,0), ![]() D. (2,0),
D. (2,0), ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学活动课上,老师要求学生在5×5的正方形ABCD网格中(小正方形的边长为1)画直角三角形,要求三个顶点都在格点上,而且三边与AB或AD都不平行.画四种图形,并直接写出其周长(所画图象相似的只算一种). 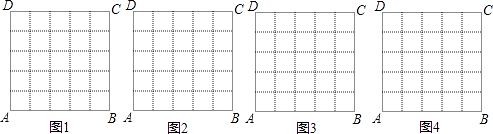
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆货车和一辆小轿车同时从甲地出发,货车匀速行驶至乙地,小轿车中途停车休整2h后提速行驶至乙地.设行驶时间为x( h),货车的路程为y1( km),小轿车的路程为y2( km ),图中的线段OA与折线OBCD分别表示y1,y2与x之间的函数关系.
(1)甲乙两地相距_____km,m=_____;
(2)求线段CD所在直线的函数表达式;
(3)小轿车停车休整后还要提速行驶多少小时,与货车之间相距20km?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为Q(2,﹣1),且与y轴交于点C(0,3),与x轴交于A,B两点(点A在点B的右侧),点P是该抛物线上的一动点,从点C沿抛物线向点A运动(点P与A不重合),过点P作PD∥y轴,交AC于点D.
(1)求该抛物线的函数关系式;
(2)当△ADP是直角三角形时,求点P的坐标;
(3)在题(2)的结论下,若点E在x轴上,点F在抛物线上,问是否存在以A、P、E、F为顶点的平行四边形?若存在,求点F的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com