
【题目】下列说法正确的是( )
A.必然事件发生的概率为0
B.一组数据1,6,3,9,8的极差为7
C.“面积相等的两个三角形全等”这一事件是必然事件
D.“任意一个三角形的外角和等于180°”这一事件是不可能事件
科目:初中数学 来源: 题型:
【题目】某校七年级学生开展踢毽子比赛活动,每班派5名同学参加,按团体总分多少排列名次,在规定的时间内每人踢100个以上(含100)为优秀.下表是甲班和乙班成绩最好的5名学生的比赛数据(单位:个)
1号 | 2号 | 3号 | 4号 | 5号 | 合计 | |
甲 | 100 | 98 | 110 | 89 | 103 | 500 |
乙 | 89 | 100 | 95 | 119 | 97 | 500 |
统计发现两班总分相等,S![]()
![]() S
S![]() , 此时有同学建议,可以通过考查数据中的其他信息作为参考,请你解答下列问题:
, 此时有同学建议,可以通过考查数据中的其他信息作为参考,请你解答下列问题:
(1)计算两班的优秀率;
(2)求两班比赛数据的中位数;
(3)根椐以上信息,你认为应该把冠军奖状发给哪一个班?简述理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
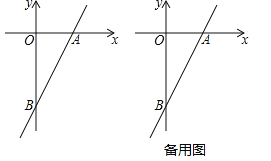
【题目】已知一次函数![]() 的图象与x轴、y轴分别相交于点A、B,点P在该函数的图象上,P到x轴、y轴的距离分别为
的图象与x轴、y轴分别相交于点A、B,点P在该函数的图象上,P到x轴、y轴的距离分别为![]() 、
、![]() .
.
(1)当P为线段AB的中点时,求![]() 的值;
的值;
(2)直接写出![]() 的范围,并求当
的范围,并求当![]() 时点P的坐标;
时点P的坐标;
(3)若在线段AB上存在无数个P点,使![]() (a为常数),求a的值.
(a为常数),求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,梯形OABC中,O为直角坐标系的原点,A、B、C的坐标分别为(14,0)、(14,3)、(4,3).点P、Q同时从原点出发,分别作匀速运动,其中点P沿OA向终点A运动,速度为每秒1个单位;点Q沿OC、CB向终点B运动,当这两点中有一点到达自己的终点时,另一点也停止运动.设P从出发起运动了t秒.
(1)如果点Q的速度为每秒2个单位,①试分别写出这时点Q在OC上或在CB上时的坐标(用含t的代数式表示,不要求写出t的取值范围);
②求t为何值时,PQ∥OC?
(2)如果点P与点Q所经过的路程之和恰好为梯形OABC的周长的一半,①试用含t的代数式表示这时点Q所经过的路程和它的速度;
②试问:这时直线PQ是否可能同时把梯形OABC的面积也分成相等的两部分?如有可能,求出相应的t的值和P、Q的坐标;如不可能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明从家出发(记为原点0)向东走3m,他把数轴上+3的位置记为点A,他又东走了5m,记为点B,点B表示什么数?接着他又向西走了10m到点C,点C表示什么数?请你画出数轴,并在数轴上标出点A、点B的位置,这时如果小明要回家,则小明应如何走?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;其中正确结论的为(请将所有正确的序号都填上).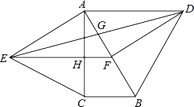
查看答案和解析>>
科目:初中数学 来源: 题型:
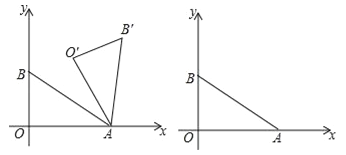
【题目】如图,在平面直角坐标系xOy中,一次函数![]() 的图象与x轴、y轴分别交于点A、B,把Rt△AOB绕点A顺时针旋转角α(30°<α<180°),得到△AO′B′.
的图象与x轴、y轴分别交于点A、B,把Rt△AOB绕点A顺时针旋转角α(30°<α<180°),得到△AO′B′.
(1)当α=60°时,判断点B是否在直线O′B′上,并说明理由;
(2)连接OO′,设OO′与AB交于点D,当α为何值时,四边形ADO′B′是平行四边形?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com