解:(1)∵抛物线y=x
2-bx与x轴正半轴相交于点A,
∴y=0时,得x
1=0,x
2=b,
∴A(b,0),且b>0,
∴OA=b,
∵△OAB的面积等于6,B(m,-3),
得S
△OAB=

3•b=6,
解得:b=4.
∴A(4,0),抛物线的表达式为y=x
2-4x,
∵点B(m,-3)在抛物线y=x
2-4x上,
∴m
2-4m=-3.
解得:m
1=1,m
2=3.
∴点B的坐标为(1,-3)或(3,-3).
(2)∵y=x
2-4x=(x-2)
2-4,
∴抛物线的顶点为C(2,-4),对称轴为直线x=2,
设P(2,n).即得PO=

,
当⊙P与⊙C相切时,有外切或内切两种情况,并且n>-4.
①如果⊙P与⊙C外切,那么 PC=PO+2.
即得 n+4=

+2,
解得 n=0,
∴P(2,0).
②如果⊙P与⊙C内切,那么 PC=PO-2.
即得 n+4=

-2,
解得 n=-

,
∴P(2,
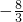
).
∴所求点P的坐标为(2,0)、(2,
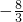
).
分析:(1)根据抛物线y=x
2-bx与x轴正半轴相交,得出A的坐标,求出OA的值,再根据△OAB的面积等于6,B(m,-3),得出b的值,即可求出抛物线的表达式,再根据点B(m,-3)在抛物线上,从而求出m的值,求出B点的坐标;
(2)把抛物线y=x
2-4x进行整理,得出顶点坐标和对称轴,再设出P点的坐标,得出PO的值,再分两种情况讨论,当⊙P与⊙C外切和果⊙P与⊙C内切时,分别求出PC的值,得出n的值,即可求出点P的坐标.
点评:此题考查了二次函数的综合,用到的知识点有抛物线的顶点公式和三角形的面积求法.在求有关动点问题时要注意分析题意分情况讨论结果,不要漏掉.

 已知:抛物线y=x2-bx与x轴正半轴相交于点A,点B(m,-3)为抛物线上一点,△OAB的面积等于6.
已知:抛物线y=x2-bx与x轴正半轴相交于点A,点B(m,-3)为抛物线上一点,△OAB的面积等于6. 3•b=6,
3•b=6, ,
, +2,
+2, -2,
-2, ,
,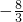 ).
).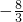 ).
).

 阅读快车系列答案
阅读快车系列答案