
【题目】如图,AB是⊙O的直径,AC是⊙O的弦,过点C的切线交AB的延长线于点D,若∠A=∠D,CD=3,则图中阴影部分的面积为 . 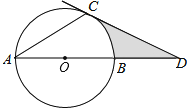
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】某食品厂从生产的袋装食品中抽出样品 20 袋,检测每袋的质量是否符合标准,超过或不足的部分分别用正、负数来表示,记录如下表:

①这批样品的平均质量比标准质量多还是少?用你学过的方法合理解释;
②若标准质量为 450 克,则抽样检测的总质量是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知A、O、B三点在同一直线上,射线OD、OE分别平分∠AOC、∠BOC
(1)求∠DOE的度数;
(2)如图2,在∠AOD内引一条射线OF,使∠COF=![]() ,其他不变,设∠DOF=
,其他不变,设∠DOF=![]()
![]() )
)
①求∠AOF的度数(用含![]() 的代数式表示).
的代数式表示).
②若∠BOD是∠AOF的2倍,求∠DOF的度数.
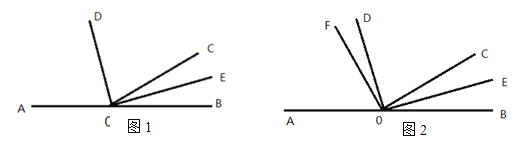
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,点D,E分别在AB,AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CF,连接EF.
(1)补充完成图形;
(2)若EF∥CD,求证:∠BDC=90°.
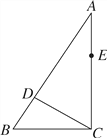
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边△ABC中:
(1)如图1,P,Q是BC边上的两点,AP=AQ,∠BAP=20°,求∠AQB的度数;
(2)点P,Q是BC边上的两个动点(不与点B,C重合),点P在点Q的左侧,且AP=AQ,点Q关于直线AC的对称点为M,连接AM,PM.
①依题意将图2补全;
②小茹通过观察、实验提出猜想:在点P,Q运动的过程中,始终有PA=PM,小茹把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:要证明PA=PM,只需证△APM是等边三角形;
想法2:在BA上取一点N,使得BN=BP,要证明PA=PM,只需证△ANP≌△PCM;
想法3:将线段BP绕点B顺时针旋转60°,得到线段BK,要证PA=PM,只需证PA=CK,PM=CK…
请你参考上面的想法,帮助小茹证明PA=PM(一种方法即可).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是四边形ABCD外接圆上任意一点,且不与四边形顶点重合,若AD是⊙O的直径,AB=BC=CD.连接PA,PB,PC,若PA=a,则点A到PB和PC的距离之和AE+AF= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解学生大课间活动的跳绳情况,随机抽取了50名学生每分钟跳绳的次数进行统计,把统计结果绘制成如表和直方图.
次数 | 70≤x<90 | 90≤x<110 | 110≤x<130 | 130≤x<150 | 150≤x<170 |
人数 | 8 | 23 | 16 | 2 | 1 |
根据所给信息,回答下列问题:
(1)本次调查的样本容量是;
(2)本次调查中每分钟跳绳次数达到110次以上(含110次)的共有的共有人;
(3)根据上表的数据补全直方图;
(4)如果跳绳次数达到130次以上的3人中有2名女生和一名男生,学校从这3人中抽取2名学生进行经验交流,求恰好抽中一男一女的概率(要求用列表法或树状图写出分析过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:①AD∥BC;②∠ACB=2∠ADB;③![]() ;④BD平分∠ADC;⑤∠BDC=
;④BD平分∠ADC;⑤∠BDC=![]() ∠BAC.其中正确的结论有_______个.
∠BAC.其中正确的结论有_______个.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com