
| 1.310-1.39 |
| 0.3 |
| 1.310-1.39 |
| 0.3 |
| 1.310-1.39 |
| 0.3 |
| 1.310-1 |
| 0.3 |
| 10×9 |
| 2 |
| 1.0510-1 |
| 0.05 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:阅读理解
|
|
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
查看答案和解析>>
科目:初中数学 来源: 题型:
|
查看答案和解析>>
科目:初中数学 来源:2011-2012学年北京市西城区九年级第一学期期末测试数学卷 题型:解答题
阅读下列材料:
题目:已知实数a,x满足a>2且x>2,试判断 与
与 的大小关系,并加以说明.
的大小关系,并加以说明.
思路:可用“求差法”比较两个数的大小,先列出 与
与 的差
的差 ,再
,再
说明y的符号即可.[来源:Z。xx。k.Com]
现给出如下利用函数解决问题的方法:
简解:可将y的代数式整理成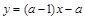 ,要判断y的符号可借助函数
,要判断y的符号可借助函数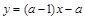 的图象和性质解决.
的图象和性质解决.
参考以上解题思路解决以下问题:
已知a,b,c都是非负数,a<5,且 ,
, .
.
【小题1】(1)分别用含a的代数式表示4b,4c;
【小题2】(2)说明a,b,c之间的大小关系.
查看答案和解析>>
科目:初中数学 来源:2012届北京市西城区九年级第一学期期末测试数学卷 题型:解答题
阅读下列材料:
题目:已知实数a,x满足a>2且x>2,试判断 与
与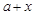 的大小关系,并加以说明.
的大小关系,并加以说明.
思路:可用“求差法”比较两个数的大小,先列出 与
与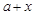 的差
的差 ,再
,再
说明y的符号即可.[来源:Z。xx。k.Com]
现给出如下利用函数解决问题的方法:
简解:可将y的代数式整理成 ,要判断y的符号可借助函数
,要判断y的符号可借助函数 的图象和性质解决.
的图象和性质解决.
参考以上解题思路解决以下问题:
已知a,b,c都是非负数,a<5,且  ,
, .
.
1.(1)分别用含a的代数式表示4b,4c;
2.(2)说明a,b,c之间的大小关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com