
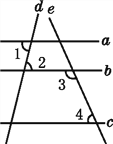
【题目】如图,已知直线a,b,c,d,e,且∠1=∠2,∠3+∠4=180°,则a与c平行吗?为什么?
解:a与c平行.
理由:因为∠1=∠2( ),
所以a∥b ( ).
因为∠3+∠4=180°( ),
所以b∥c ( ).
所以a∥c ( ).
科目:初中数学 来源: 题型:
【题目】列方程解应用题:某人出差带回了外地的某种特产若干袋,分给朋友们品尝,如果每人分5袋,还余3袋;如果每人分6袋,还差3袋.问这人带回特产共多少袋?一共分给了多少个朋友?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道:分式和分数有着很多的相似点.如类比分数的基本性质,我们得到了分式的基本性质;类比分数的运算法则,我们得到了分式的运算法则,等等.小学里,把分子比分母小的分数叫做真分数.类似地,我们把分子整式的次数小于分母整式的次数的分式称为真分式;反之,称为假分式.对于任何一个假分式都可以化成整式与真分式的和的形式, 如: ![]() =
= ![]() =
= ![]() +
+ ![]() =1+
=1+ ![]() ;
;![]() =
= ![]() =
= ![]() +
+ ![]() =2+(﹣
=2+(﹣ ![]() ).
).
(1)下列分式中,属于真分式的是:(填序号); ① ![]()
② ![]()
③ ![]()
④ ![]()
(2)将假分式 ![]() 化成整式与真分式的和的形式为:
化成整式与真分式的和的形式为: ![]() =+ , 若假分式
=+ , 若假分式 ![]() 的值为正整数,则整数a的值为;
的值为正整数,则整数a的值为;
(3)将假分式 ![]() 化成整式与真分式的和的形式:
化成整式与真分式的和的形式: ![]() = .
= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
(1)如图1,四边形ABCD是正方形,点E、点F分别在边AB和AD上,且AE=AF.此时,线段BE、DF的数量关系是 , 位置关系是 . 请直接写出结论.
(2)如图2,等腰直角三角形FAE绕直角顶点A顺时针旋转∠α,当0°<α<90°时,连接BE、DF,此时(1)中的结论是否成立,如果成立,请证明;如果不成立,请说明理由.
(3)如图3,等腰直角三角形FAE绕直角顶点A顺时针旋转∠α,当α=90°时,连接BE、DF,若正方形的边长为1,猜想当AE=时,直线DF垂直平分BE.请写出计算过程.
(4)如图4,等腰直角三角形FAE绕直角顶点A顺时针旋转∠α,当90°<α<180°时,连接BD、DE、EF、FB得到四边形BDEF,则顺次连接四边形BDEF各边中点所组成的四边形是什么特殊四边形?请直接写出结论: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的有
①![]() 的算术平方根是5
的算术平方根是5
②关于x的方程m![]() +2x+1=0没有实数根,那么m的取值范围是m>1且m≠0.
+2x+1=0没有实数根,那么m的取值范围是m>1且m≠0.
③一组数据:1,1,3,3的方差是![]() .
.
④已知三角形的两边长分别为3和4,则第三边长c的取值范围是1<c<7.
⑤在平行四边形、线段、角、等边三角形四个图形中,既是轴对称图形又是中心对称图的只有一个.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,一元二次方程x2﹣8x+15=0的两根分别是⊙O1和⊙O2的半径,当⊙O1和⊙O2相切时,O1O2的长度是( )
A.2
B.8
C.2或8
D.2<O1O2<8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com