
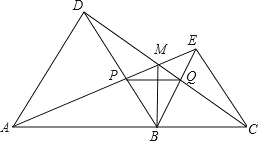
【题目】如图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q,连接PQ,BM,下面结论:
①△ABE≌△DBC;②∠DMA=60°;③△BPQ为等边三角形;④MB平分∠AMC,
其中结论正确的有( )
A.1个
B.2个
C.3个
D.4个
【答案】D
【解析】
试题分析:∵△ABD、△BCE为等边三角形,
∴AB=DB,∠ABD=∠CBE=60°,BE=BC,
∴∠ABE=∠DBC,∠PBQ=60°,
在△ABE和△DBC中,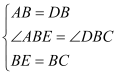 ,
,
∴△ABE≌△DBC(SAS),
∴①正确;
∵△ABE≌△DBC,
∴∠BAE=∠BDC,
∵∠BDC+∠BCD=180°﹣60°﹣60°=60°,
∴∠DMA=∠BAE+∠BCD=∠BDC+∠BCD=60°,
∴②正确;
在△ABP和△DBQ中,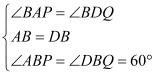 ,
,
∴△ABP≌△DBQ(ASA),∴BP=BQ,∴△BPQ为等边三角形,
∴③正确;∵∠DMA=60°,∴∠AMC=120°,∴∠AMC+∠PBQ=180°,
∴P、B、Q、M四点共圆,∵BP=BQ,∴![]() ,∴∠BMP=∠BMQ,
,∴∠BMP=∠BMQ,
即MB平分∠AMC;∴④正确;
综上所述:正确的结论有4个;
故选:D.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ACB中,∠ACB=90°,AC=3,BC=4,有一过点C的动圆⊙O与斜边AB相切于动点P,连接CP.
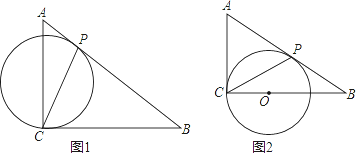
(1)当⊙O与直角边AC相切时,如图2所示,求此时⊙O的半径r的长;
(2)随着切点P的位置不同,弦CP的长也会发生变化,试求出弦CP的长的取值范围.
(3)当切点P在何处时,⊙O的半径r有最大值?试求出这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙E的圆心E(3,0),半径为5,⊙E与y轴相交于A、B两点(点A在点B的上方),与x轴的正半轴相交于点C;直线l的解析式为y=![]() x+4,与x轴相交于点D;以C为顶点的抛物线经过点B.
x+4,与x轴相交于点D;以C为顶点的抛物线经过点B.
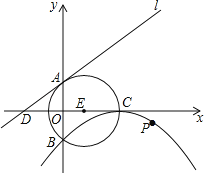
(1)求抛物线的解析式;
(2)判断直线l与⊙E的位置关系,并说明理由;
(3) 动点P在抛物线上,当点P到直线l的距离最小时,求出点P的坐标及最小距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工程承包方指定由甲、乙两个工程队完成某项工程,若由甲工程队单独做需要40天完成,现在甲、乙两个工程队共同做20天后,由于甲工程队另有其它任务不再做该工程,剩下工程由乙工程队再单独做了20天才完成任务.
(1)求乙工程队单独完成该工程需要多少天?
(2)如果工程承包方要求乙工程队的工作时间不能超过30天,要完成该工程,甲工程队至少要工作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有A、B两个口袋,A口袋中装有两个分别标有数字2,3的小球;B口袋中装有三个分别标有数字3,4,5的小球.小明先从A口袋中随机取出-个小球,再从B口袋中随机取出一个小球;
(1)用树状图法或列表法表示小明所取出的二个小球的和为奇数的概率.
(2)若从A口袋中取出的小球记为x,从B口袋中取出的小球记为y,则点M(x,y)落在直线y=x+1上的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com