

分析 (1)过P作PE∥AB,根据平行线的性质可求得∠BPD=∠B+∠D;
(2)过B作BF∥CD,结合(1)的结论和平行线的性质可得到∠BPD=∠ABP+∠D+∠BQD;
(3)根据三角形内角与外角的关系可得∠A+∠F=∠1,∠B+∠G=∠2,进而可得∠A+∠F+∠B+∠G=∠1+∠2,再根据多边形内角和可得答案.
解答 解:(1)∠BPD=∠B+∠D;
过P作PE∥AB,
∵AB∥CD,
∴PE∥AB∥CD,
∴∠1=∠ABP,∠2=∠CDP,
∴∠BPD=∠B+∠D;
(2)延长BP交CD于E,
∵∠B+∠BQD=∠BED,∠D+∠BED=∠BPD,
∴∠B+∠D+∠BQD=∠BPD;
故答案为:∠B+∠D+∠BQD=∠BPD.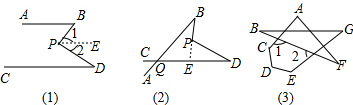
(3)∵∠A+∠F=∠1,∠B+∠G=∠2,
∴∠A+∠F+∠B+∠G=∠1+∠2,
∵∠1+∠2+∠C+∠D+∠E=540°,
∴∠A+∠F+∠B+∠G+∠C+∠D+∠E=540°.
点评 本题主要考查平行线的性质,三角形形内角与外角的关系,关键是掌握三角形的外角等于与它不相邻的两个内角的和.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:初中数学 来源: 题型:填空题
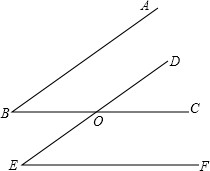 如图,已知:BC交DE于O,给出下面三个论断:①∠B=∠E;②AB∥DE;③BC∥EF.请以其中的两个论断为条件,填入“题设”栏中,以一个论断为结论,填入“结论”栏中,使之成为一个正确的命题,并加以证明.
如图,已知:BC交DE于O,给出下面三个论断:①∠B=∠E;②AB∥DE;③BC∥EF.请以其中的两个论断为条件,填入“题设”栏中,以一个论断为结论,填入“结论”栏中,使之成为一个正确的命题,并加以证明.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2不是单项式 | B. | -ab2的系数是-1,次数是3 | ||
| C. | 6πx3的系数是6 | D. | -$\frac{{2{x^2}y}}{3}$的系数是-2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com