
【题目】如图,抛物线y=ax2+bx﹣2经过点A(1,0)和点B(4,0),与y轴交于点C.
附:阅读材料
法国弗朗索瓦韦达最早发现一元二次方程中根与系数的关系为:两根之和等于一次项系数与二次项系数之比的相反数,两根之积等于常数项羽二次项系数之比,人们称之为韦达定理.
即:设一元二次方程ax2+bx+c=0的两根为x1、x2 , 则:x1+x2=﹣ ![]() ,x1x2=
,x1x2= ![]() 能灵活运用韦达定理,有时可以使解题更为简单.
能灵活运用韦达定理,有时可以使解题更为简单.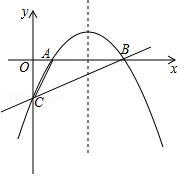
(1)求抛物线的解析式;
(2)以点A为圆心,作于直线BC相切的⊙A,求⊙A的面积;
(3)将直线BC向下平移n个单位后与抛物线交于点M、N,且线段MN=2CB,求直线MN的解析式及平移距离.
【答案】
(1)
解:设抛物线解析式为y=a(x﹣1)(x﹣4),
即y=ax2﹣5ax+4a,
∴4a=﹣2,解得a=﹣ ![]() ,
,
∴抛物线解析式为y=﹣ ![]() x2+
x2+ ![]() x﹣2;
x﹣2;
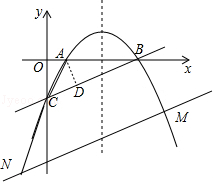
(2)
解:作AD⊥BC于D,如图,当x=0时,y=﹣ ![]() x2+
x2+ ![]() x﹣2=﹣2,则C(0,﹣2),
x﹣2=﹣2,则C(0,﹣2),
BC= ![]() =2
=2 ![]() ;
;
∵∠ABD=∠CBO,
∴Rt△BAD∽Rt△BCO,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴AD= ![]() ,
,
∵直线BC相切的⊙A,
∴AD为⊙A的半径,
∴⊙A的面积=π( ![]() )2=
)2= ![]() π;
π;
(3)
解:设直线BC的解析式为y=kx+m,
把B(4,0),C(0,﹣2)代入得 ![]() ,解得
,解得  ,
,
∴直线BC的解析式为y= ![]() x﹣2,
x﹣2,
设直线MN的解析式为y= ![]() x+t,M(x1,y1),N(x2,y2),
x+t,M(x1,y1),N(x2,y2),
则x1、x2为方程﹣ ![]() x2+
x2+ ![]() x﹣2=
x﹣2= ![]() x+2t的两根,
x+2t的两根,
方程整理为x2﹣4x+2t+4=0,
∴x1+x2=4,x1x2=2t+4,
∵y1﹣y2= ![]() x1+t﹣(
x1+t﹣( ![]() x2+t)=
x2+t)= ![]() (x1﹣x2),
(x1﹣x2),
∴MN= ![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
∵MN=2CB,
∴ ![]() =4
=4 ![]() ,解得t=﹣8,
,解得t=﹣8,
∴直线MN的解析式为y= ![]() x﹣8,
x﹣8,
∴将直线BC向下平移6个单位得到直线MN,即平移的距离为6.
【解析】(1)设交点式y=a(x﹣1)(x﹣4),即y=ax2﹣5ax+4a,然后利用4a=﹣2求出a即可得到抛物线解析式;(2)作AD⊥BC于D,如图,先确定C(0,﹣2),计算出BC=2 ![]() ,再证明Rt△BAD∽Rt△BCO,利用相似比可计算出AD=
,再证明Rt△BAD∽Rt△BCO,利用相似比可计算出AD= ![]() ,然后利用切线的性质得到圆的半径为AD,再利用圆的面积公式求解;(3)先利用待定系数法确定直线BC的解析式为y=
,然后利用切线的性质得到圆的半径为AD,再利用圆的面积公式求解;(3)先利用待定系数法确定直线BC的解析式为y= ![]() x﹣2,则可设直线MN的解析式为y=
x﹣2,则可设直线MN的解析式为y= ![]() x+t,M(x1 , y1),N(x2 , y2),利用两函数的交点问题得到x1、x2为方程﹣
x+t,M(x1 , y1),N(x2 , y2),利用两函数的交点问题得到x1、x2为方程﹣ ![]() x2+
x2+ ![]() x﹣2=
x﹣2= ![]() x+2t的两根,利用根与系数的关系得x1+x2=4,x1x2=2t+4,则y1﹣y2=
x+2t的两根,利用根与系数的关系得x1+x2=4,x1x2=2t+4,则y1﹣y2= ![]() (x1﹣x2),接着利用两点间的距离公式和完全平方公式得到MN=
(x1﹣x2),接着利用两点间的距离公式和完全平方公式得到MN= ![]() =
= ![]() ,所以
,所以 ![]() =4
=4 ![]() ,解方程得到t的值,从而得到直线MN的解析式,然后利用直线平移的规律确定平移的距离.
,解方程得到t的值,从而得到直线MN的解析式,然后利用直线平移的规律确定平移的距离.
【考点精析】本题主要考查了根与系数的关系和确定一次函数的表达式的相关知识点,需要掌握一元二次方程ax2+bx+c=0(a≠0)的根由方程的系数a、b、c而定;两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商;确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】为了维护海洋权益,新组建的国家海洋局加大了在南海的巡逻力度,一天,我两艘海监船刚好在我某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍的船只停在C处海域.如图所示,AB=60( ![]() )海里,在B处测得C在北偏东45°的方向上,A处测得C在北偏西30°的方向上,在海岸线AB上有一灯塔D,测得AD=120(
)海里,在B处测得C在北偏东45°的方向上,A处测得C在北偏西30°的方向上,在海岸线AB上有一灯塔D,测得AD=120( ![]() )海里.
)海里.
(1)分别求出A与C及B与C的距离AC、BC(结果保留根号)
(2)已知在灯塔D周围100海里范围内有暗礁群,我在A处海监船沿AC前往C处盘查,图中有无触礁的危险?
(参考数据: ![]() =1.41,
=1.41, ![]() =1.73,
=1.73, ![]() =2.45)
=2.45)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l:y= ![]() x+1交x轴于点A,交y轴于点B,点A1、A2、A3 , …在x轴的正半轴上,点B1、B2、B3 , …在直线l上.若△OB1A1 , △A1B2A2 , △A2B3A3 , …均为等边三角形,则△A6B7A7的周长是 .
x+1交x轴于点A,交y轴于点B,点A1、A2、A3 , …在x轴的正半轴上,点B1、B2、B3 , …在直线l上.若△OB1A1 , △A1B2A2 , △A2B3A3 , …均为等边三角形,则△A6B7A7的周长是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在图1﹣﹣图4中,菱形ABCD的边长为3,∠A=60°,点M是AD边上一点,且DM= ![]() AD,点N是折线AB﹣BC上的一个动点.
AD,点N是折线AB﹣BC上的一个动点.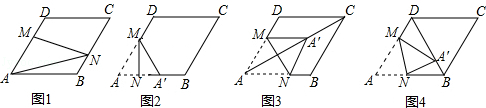
(1)如图1,当N在BC边上,且MN过对角线AC与BD的交点时,则线段AN的长度为 .
(2)当点N在AB边上时,将△AMN沿MN翻折得到
△A′MN,如图2,
①若点A′落在AB边上,则线段AN的长度为 ![]() ;
;
②当点A′落在对角线AC上时,如图3,求证:四边形AM A′N是菱形;
③当点A′落在对角线BD上时,如图4,求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形AOCB的两边OA、OC分别在x轴和y轴上,且OA=1,OC= ![]() ,在第二象限内,以原点O为位似中心将矩形AOCB放大为原来的
,在第二象限内,以原点O为位似中心将矩形AOCB放大为原来的 ![]() 倍,得到矩形A1OC1B1 , 再以原点O为位似中心将矩形A1OC1B1放大为原来的
倍,得到矩形A1OC1B1 , 再以原点O为位似中心将矩形A1OC1B1放大为原来的 ![]() 倍,得到矩形A2OC2B2…,以此类推,得到的矩形A100OC100B100的对角线交点的纵坐标为 .
倍,得到矩形A2OC2B2…,以此类推,得到的矩形A100OC100B100的对角线交点的纵坐标为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在已知的△ABC中,按以下步骤作图: ①分别以B,C为圆心,以大于 ![]() BC的长为半径作弧,两弧相交于两点M,N;
BC的长为半径作弧,两弧相交于两点M,N;
②作直线MN交AB于点D,连接CD.
若CD=AC,∠A=50°,则∠ACB的度数为( )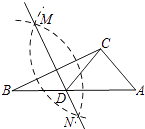
A.90°
B.95°
C.100°
D.105°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,地面上两个村庄C、D处于同一水平线上,一飞行器在空中以6千米/小时的速度沿MN方向水平飞行,航线MN与C、D在同一铅直平面内.当该飞行器飞行至村庄C的正上方A处时,测得∠NAD=60°;该飞行器从A处飞行40分钟至B处时,测得∠ABD=75°.求村庄C、D间的距离( ![]() 取1.73,结果精确到0.1千米)
取1.73,结果精确到0.1千米) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以x为自变量的二次函数y=x2﹣2(b﹣2)x+b2﹣1的图象不经过第三象限,则实数b的取值范围是( )
A.b≥ ![]()
B.b≥1或b≤﹣1
C.b≥2
D.1≤b≤2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com