
在平面直角坐标系中,Rt△AOB的位置如图所示,已知∠AOB=90°,AO=BO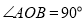 ,点A的坐标为(-3,1).(1)、求点B的坐标;(2)、求过A、O、B三点的抛物线的解析式;(3)、设点P为抛物线上到X轴的距离为1的点,点B关于抛物线的对称轴
,点A的坐标为(-3,1).(1)、求点B的坐标;(2)、求过A、O、B三点的抛物线的解析式;(3)、设点P为抛物线上到X轴的距离为1的点,点B关于抛物线的对称轴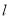 的对称点为
的对称点为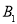 , 求点P的坐标和
, 求点P的坐标和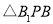 的面积.
的面积.
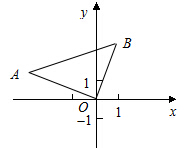
(1)、B(1,3);(2)、y=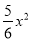 +
+ ;(3)、
;(3)、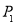
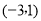 、
、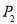
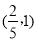 、
、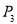
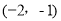 、
、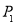
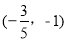
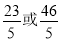
【解析】
试题分析:(1)、分别作AC⊥x轴于C,BD⊥x轴于D,证明△ACO和△BOD全等从而求出点B的坐标;(2)、利用待定系数法求出函数解析式;(3)、首先求出对称轴方程,然后根据对称的性质求出点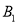 的坐标,设出点P的坐标为(k,1)和(k,-1),将P点坐标代入函数解析式求出k的值,然后计算三角形的面积.
的坐标,设出点P的坐标为(k,1)和(k,-1),将P点坐标代入函数解析式求出k的值,然后计算三角形的面积.
试题解析:(1)、作AC⊥x轴于C,作BD⊥x轴于D.
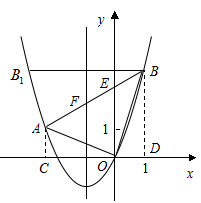
则∠ACO=∠ODB=90°, ∴∠AOC+∠OAC=90°. 又∵∠AOB=90°, ∴∠AOC+∠BOD=90°
∴∠OAC=∠BOD 又∵AO=BO ∴△ACO≌△ODB ∴OD=AC=1 DB=OC=3 ∴点B的坐标为(1,3).
(2)、因为抛物线过原点,故可设所求抛物线的解析式为: .将
.将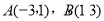 两点代入,得
两点代入,得
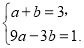 解得
解得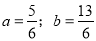 . 故所求抛物线的解析式为
. 故所求抛物线的解析式为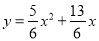 .
.
(3)、在抛物线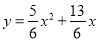 中,对称轴
中,对称轴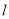 的方程是
的方程是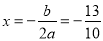 .
.
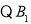 是
是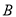 关于抛物线的对称轴
关于抛物线的对称轴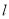 的对称点,故
的对称点,故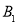 坐标
坐标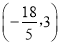 ,
, 
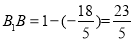
由题意,设抛物线上到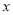 轴的距离为1的点为
轴的距离为1的点为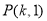 或
或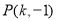 ,则
,则
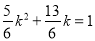 或
或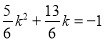 即:
即: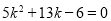 或
或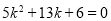
解得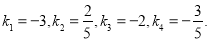
即抛物线上到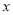 轴的距离为1的点为:
轴的距离为1的点为: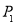
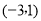 、
、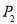
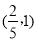 、
、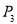
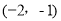 、
、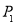
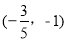 .
.
在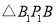 中,底边
中,底边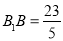 ,高的长为2,故
,高的长为2,故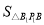
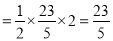 ,
,
同理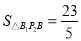 ,
,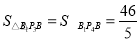
考点:二次函数的性质.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源:2014-2015学年江苏省如皋市开发区九年级上学期第三次质量检测数学试卷(解析版) 题型:填空题
如图,AB为⊙O的直径,点C,D在⊙O上.若∠AOD=30°,则∠BCD的度数是 .

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省九年级上学期期末考试数学试卷(解析版) 题型:解答题
(本题满分10分)如图,二次函数y=-x2+nx+n2-9(n为常数)的图像经过坐标原点和x轴上另一点A,顶点在第一象限.

(1)求n的值和点A坐标;
(2)已知一次函数y=-2x+b(b >0)分别交x轴、y轴于M、N两点.点P是二次函数图像的y轴右侧部分上的一个动点,若PN⊥NM于N点,且△PMN与△OMN相似,求点P坐标.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年广东省九年级上学期期末考试数学试卷(解析版) 题型:解答题
如图,在边长为1的小正方形组成的方格纸上,将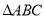 绕着点
绕着点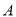 顺时针旋转
顺时针旋转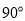 ,
,

(1)画出旋转后的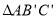 ;
;
(2)求线段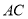 在旋转过程中所扫过的扇形面积。
在旋转过程中所扫过的扇形面积。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年广东省九年级上学期期末考试数学试卷(解析版) 题型:填空题
如图,已知OA,OB是⊙O的两条半径,且OA⊥OB,点C在圆周上(与点A、B不重合),则∠ACB的度数为 .

查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省尤溪县九年级上学期期末学习效果评价数学试卷(解析版) 题型:解答题
阳光通过窗口照到教室内,竖直窗框在地面上留下2.1m长的影子(如图),已知窗框的影子DE到窗下墙脚的距离CE=3.9m,窗口底边离地面的距离BC=1.2m,试求窗口的高度(即AB的值)
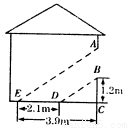
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com