
分析 (1)分别过D、E作DG⊥BC,EH⊥BC,垂足分别为G、H,在△EHC中可求得EH,CH,在Rt△DBG中可求得BD,当D和M重合时可知正方形的边长为DG,可求得CP的长,求得t;
(2)分0<t≤9、9<t≤17、17<t≤23、23<t≤29、29<t≤35五种情况,结合条件分别确定出重叠部分的图形,再求得其面积即可;
(3)分三种情形①如图7中,当∠DA′M=90°时,作MH⊥AA′于H,AA′交DE于R.②如图8中,当M与R重合时,∠DMA′=90°,此时t=9.③如图9中,当∠MDA′=90°时,作MH⊥ED于H.利用相似三角形的性质,列出方程分别求解即可.
解答 解:(1)如图1,分别过D、E作DG⊥BC,EH⊥BC,垂足分别为G、H,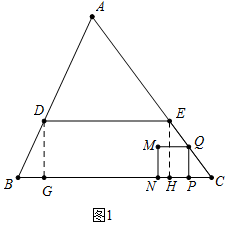
在Rt△CEH中,CE=15,cosC=$\frac{3}{5}$,
∴$\frac{HC}{EC}$=$\frac{3}{5}$,即$\frac{HC}{15}$=$\frac{3}{5}$,解得HC=9,
由勾股定理可求得EH=12,
又∵四边形DEHG为矩形,
∴DG=EH=12,GH=DE=20,
又∵BC=35,
∴CG=9+20=29,
∴BG=BC-CG=35-29=6,
在Rt△DBG中,BD2=62+122=180,
∴BD=6$\sqrt{5}$,
当M与D重合时,则可知PN=DG=12,CN=CG=GH+CH=29,
∴CP=CG-DG=29-12=17,
∴t=$\frac{17}{1}$=17,
故答案为:6$\sqrt{5}$;17;
(2)①当0<t≤9时,如图2中,即P在线段CH上时,则重叠部分为正方形PQMN,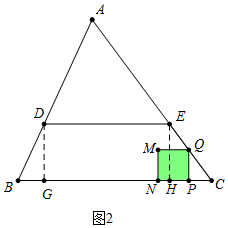
由题意可知CP=t,
∵cosC=$\frac{CP}{CQ}$,
∴$\frac{t}{CQ}$=$\frac{3}{5}$,解得CQ=$\frac{5t}{3}$,
∴PQ=$\frac{4}{3}$t,
∴S=PQ2=($\frac{4}{3}$t)2=$\frac{16}{9}$t2,
②当9<t≤17时,如图3中,此时重叠部分为正方形PQMN,且DE=20,S=PQ2=144;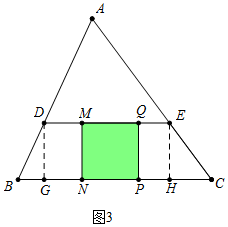
③当17<t≤23时,如图4中,此时重叠部分是五边形PQDRN,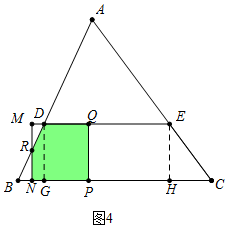
则CN=CP+PN=t+12,可求得BN=35-(t+12)=23-t,
∵MN∥DG,
∴$\frac{RN}{DG}$=$\frac{BN}{BG}$,即$\frac{RN}{12}$=$\frac{23-t}{6}$,解处RN=46-2t,
∴MR=MN-RN=12-(46-2t)=2t-34,
而MD=NG=CN-CG=t+12-29=t-17,
∴S△MDR=$\frac{1}{2}$MR•MD=$\frac{1}{2}$×(2t-34)(t-17),
∴S=S正方形PQMN-S△MRD=122-$\frac{1}{2}$×(2t-34)(t-17)=-t2+34t-145;
④当23<t≤29时,如图5中,重叠部分是四边形PQDB,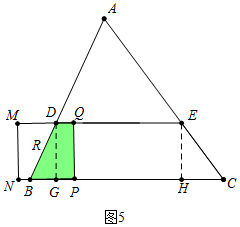
S=$\frac{1}{2}$•(DQ+PB)•PQ=6(35-t+29-t)=-12t+384.
⑤当29<t≤35时,如图6中,重叠部分是三角形PQB,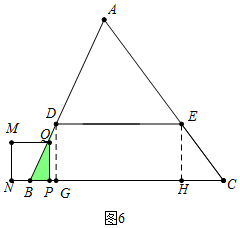
此时BP=BC-PC=35-t,且BG=6,
∵PQ∥DG,
∴$\frac{BP}{BG}$=$\frac{PQ}{DG}$,即$\frac{35-t}{6}$=$\frac{PQ}{12}$,
解得PQ=70-2t,
∴S=$\frac{1}{2}$BP•PQ=$\frac{1}{2}$(35-t)(70-2t)=(t-35)2
综上可知S=$\left\{\begin{array}{l}{\frac{16}{9}{t}^{2}}&{(0<t≤9)}\\{144}&{(9<t≤17)}\\{-{t}^{2}+34t-145}&{(17<t≤23)}\\{-12t+384}&{(23<t≤29)}\\{(t-35)^{2}}&{(29<t≤35)}\end{array}\right.$.
(3)①如图7中,当∠DA′M=90°时,作MH⊥AA′于H,AA′交DE于R.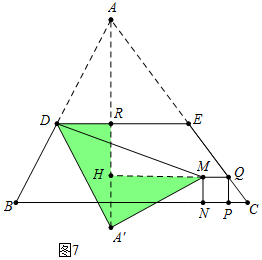
∵DE∥BC,
∴$\frac{DE}{BC}$=$\frac{AE}{AC}$,设AE=x,则有$\frac{20}{35}$=$\frac{x}{x+15}$,
∴x=20,
∴AE=20,
∵sin∠AER=sin∠C=$\frac{AR}{AE}$=$\frac{4}{5}$,
∴AR=16,ER=$\sqrt{A{E}^{2}-A{R}^{2}}$=12,
由△A′DR∽△MA′H,得$\frac{DR}{A′H}$=$\frac{A′R}{HM}$,可得$\frac{8}{\frac{4}{3}t+4}$=$\frac{16}{21-\frac{7}{3}t}$,解得t=$\frac{13}{5}$.
②如图8中,当M与R重合时,∠DMA′=90°,此时t=9.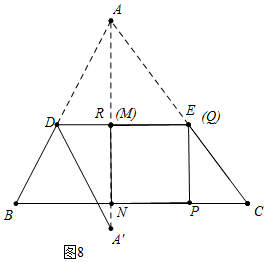
如图8′中,当∠DMA′=90°时,由△DGM∽△MHA′,得$\frac{DG}{MH}$=$\frac{GM}{A′H}$,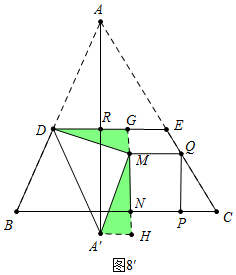
∴$\frac{8+7(3-\frac{1}{3}t)}{4+\frac{4}{3}t}$=$\frac{4(3-\frac{1}{3}t)}{7(3-\frac{1}{3}t)}$,t=$\frac{561}{65}$,
③如图9中,当∠MDA′=90°时,作MH⊥ED于H.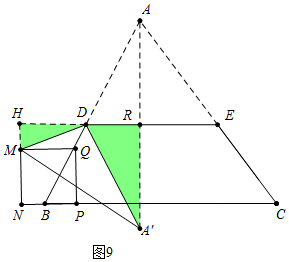
由△MDH∽△DA′R得$\frac{DH}{A′R}$=$\frac{MH}{DR}$,
∴$\frac{70-t-29}{16}$=$\frac{12-(70-2t)}{8}$,
∴t=$\frac{157}{5}$.
综上所述,t=$\frac{13}{5}$s或9s或$\frac{561}{65}$s或$\frac{157}{5}$s时,△A′DM是直角三角形.
点评 本题考查相似形综合题、正方形的性质、勾股定理、相似三角形的判定和性质、直角三角形的判定和性质等知识,解题的关键是学会正确画出图形,学会用分类讨论的思想思考问题,题目比较难,计算量比较大,属于中考压轴题.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | x-$\frac{3}{25}$=560 | B. | x+$\frac{3}{25}$=560 | C. | x-$\frac{3}{25}$x=560 | D. | x+$\frac{3}{25}$x=560 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
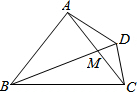 如图,在四边形ABCD中,∠BAC=∠BDC=90°,AB=AC=$\sqrt{5}$,CD=1,对角线的交点为M,则DM=$\frac{1}{2}$.
如图,在四边形ABCD中,∠BAC=∠BDC=90°,AB=AC=$\sqrt{5}$,CD=1,对角线的交点为M,则DM=$\frac{1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com