已知x1,x2是一元二次方程(a-6)x2+2ax+a=0的两个实数根.
(1)是否存在实数a,使-x1+x1x2=4+x2成立?若存在,求出a的值;若不存在,请你说明理由;
(2)求使(x1+1)(x2+1)为负整数的实数a的整数值.
解:∵x
1,x
2是一元二次方程(a-6)x
2+2ax+a=0的两个实数根,
∴由根与系数的关系可知,x
1x
2=

,x
1+x
2=-
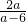
;
∵一元二次方程(a-6)x
2+2ax+a=0有两个实数根,
∴△=4a
2-4(a-6)•a≥0,且a-6≠0,
解得,a≥0,且a≠6;
(1)∵-x
1+x
1x
2=4+x
2,
∴x
1x
2=4+(x
1+x
2),即

=4-
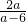
,
解得,a=24>0;
∴存在实数a,使-x
1+x
1x
2=4+x
2成立,a的值是24;
(2)∵(x
1+1)(x
2+1)=x
1x
2+(x
1+x
2)+1=

-
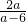
+1=-

,
∴当(x
1+1)(x
2+1)为负整数时,a-6>0,且a-6是6的约数,
∴a-6=6,a-6=3,a-6=2,a-6=1,
∴a=12,9,8,7;
∴使(x
1+1)(x
2+1)为负整数的实数a的整数值有12,9,8,7.
分析:根据根与系数的关系求得x
1x
2=

,x
1+x
2=-
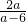
;根据一元二次方程的根的判别式求得a的取值范围;
(1)将已知等式变形为x
1x
2=4+(x
2+x
1),即

=4+
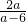
,通过解该关于a的方程即可求得a的值;
(2)根据限制性条件“(x
1+1)(x
2+1)为负整数”求得a的取值范围,然后在取值范围内取a的整数值.
点评:本题综合考查了根与系数的关系、根的判别式.注意:一元二次方程ax
2+bx+c=0(a、b、c是常数)的二次项系数a≠0.

 ,x1+x2=-
,x1+x2=-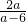 ;
; =4-
=4-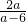 ,
, -
-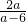 +1=-
+1=- ,
, ,x1+x2=-
,x1+x2=-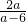 ;根据一元二次方程的根的判别式求得a的取值范围;
;根据一元二次方程的根的判别式求得a的取值范围; =4+
=4+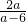 ,通过解该关于a的方程即可求得a的值;
,通过解该关于a的方程即可求得a的值;

 优加精卷系列答案
优加精卷系列答案